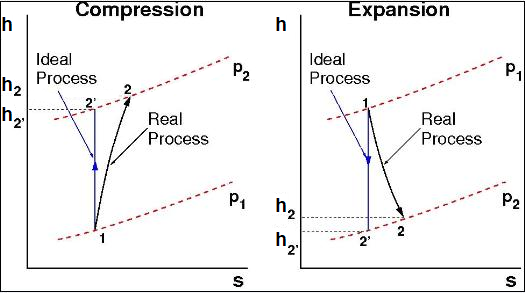
The efficiency of any device is never perfect due to both fluid dynamic and thermodynamic losses within the entire system. The losses show up in a difference in stagnation properties from the values that would be expected if the process would be perfectly isentropic. Consider the processes drawn on the T-s diagrams shown in Figure 1.2: T-s Diagrams for Compression and Expansion Processes for a compression and expansion process.
Two efficiency calculation options are possible for either process: Total to Total and Total to Static. The first option evaluates efficiency using stagnation conditions at points 1, 2 and 2’. The second option uses stagnation conditions at points 1 and 2 and static conditions at point 2’, so, the efficiency is evaluated without including the kinetic energy contribution at point 2. The Total to Total option is most useful for devices where work is either performed on the fluid (for example, a pump or compressor) or extracted from the fluid (for example, a turbine). The Total to Static option is useful for evaluating losses in devices that perform no work on the fluid (for example, diffusers and nozzles).
The isentropic work is of the form:
(1–36) |
Work is generally input for a compression process such as gas compressors, so the Total to Total isentropic efficiency is defined as the ratio of the required isentropic work to the actual required work for fluid compression:
(1–37) |
Work is usually derived from expansion processes such as steam turbines, so the Total to Total efficiency is the ratio of the actual expansion work to the isentropic expansion work:
(1–38) |
where the total enthalpy at point 1 is the mass average value of the user-selected inlet boundary condition.
In addition, the isentropic total enthalpy, is required. This is
the fluid enthalpy evaluated at the entropy at point 1 and the total
pressure at point 2. The entropy at point 1 is taken, by default,
as the mass averaged value at a user-selected inlet boundary condition.
The isentropic enthalpy is evaluated from the state equation:
(1–39) |
The isentropic enthalpy is then used in Equation 1–37 or Equation 1–38 to evaluate compression or expansion efficiency. These quantities are useful for evaluating where losses are occurring in the device. Global efficiencies reported in the solver monitor are evaluated by mass averaging the field efficiencies at the user-selected outlet boundary condition.
The Total to Static efficiency is evaluated similarly to Total to Total efficiency. The Total to Static isentropic efficiency for a compression process is:
(1–40) |
where
The Total to Static isentropic efficiency for an expansion process is:
(1–41) |
Free stream detection is also applied to the efficiency values
in a similar way to the high resolution advection blending. This is
because in the free stream the isentropic enthalpy change and the
local enthalpy change can both be small (that is, O(0)). A small number
divided by another small number can result in a noisy looking efficiency
field in inlet regions where the efficiency should be unity because
no work has yet been performed on the fluid. Free stream damping blends
the efficiency field to unity. The free stream damping is controlled
with the expert parameter fsdamp efficiency scale with a default value of 0.01. Smaller values for this parameter
will decrease the influence of the free stream damping, and reducing
it to a value of 0.0 will switch off the free stream damping completely.
Device efficiency values reported by the CFX-Solver Manager and CFD-Post macros are calculated using a boundary averaged value of the damped efficiency field variable (for example Isentropic Efficiency). In some cases, this value may be different to one calculated from the classical formula using boundary-averaged values of enthalpy. The difference is due to the field damping, and is negligible in the vast majority of cases. However, in rare cases, for example where there is localized heating or cooling, the difference may be significant and you should check the reported values with the damping disabled.