The stability criterion used for a free-floating body is the metacentric height. When the body's weight equals the weight of fluid displaced and the center of gravity and center of buoyancy are in the same vertical line, you must check the metacentric heights so that the sign of the hydrostatic restoration can be assessed.
The cut water-plane properties of a body in the equilibrium position can be used to estimate the body's metacenter. The cut water-plane area can be calculated by
(3–10) |
and the center of the cut water-plane area (center of flotation) in the fixed reference axes (FRA) is
(3–11) |
The second moments of the cut water-plane area about the center of flotation are
(3–12) |
The angle between the principal X'-axis and the positive X-axis measured counterclockwise is
(3–13) |
with respect to the principal X'- and Y'-axes,
(3–14) |
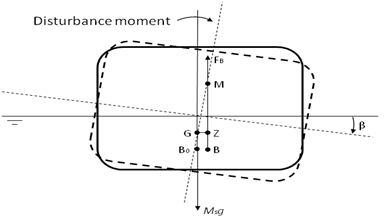
As shown in Figure 3.1: Metacenter of a Free-Floating Body, a free-floating body is in the initial
equilibrium position, the center of gravity and center of buoyancy
are at the locations of G and B0 respectively
and on the same vertical line. By turning the body through a small
angle with respect to the center of flotation, the total buoyant
force remains constant, but the center of buoyancy moves to a new
position, B. The metacenter, M, is defined as the intersection of
the body's upward buoyant force with the centerline of the body after
the body has been subjected a rotational disturbance and rotated by
a small angle. The distance , is the metacentric height.
The righting moment, balances the disturbance moment and to restores the body to its
original position if the rotational mode is stable. If
, it represents a
stable equilibrium. If
, the equilibrium is in the neutral
state. If
, the equilibrium is unstable.
The longitudinal and transverse metacentric heights are defined as
(3–15) |