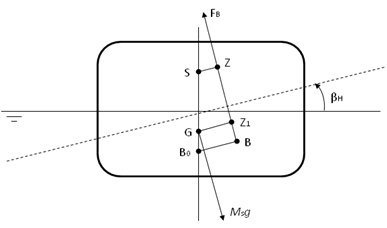
The stability at a large angle of inclination is similar to the concept applied for small angle stability. We assume that a free-floating body rotates a specified angle about a prescribed horizontal hinge axis and shifts upwards or downwards from its initial equilibrium position to ensure that the total displacement remains constant. The righting moments about this hinge axis and its perpendicular axis on the water plane are calculated and output in Aqwa.
At a known inclination angle rotated about a given horizontal
hinge axis from the original equilibrium state of a free-floating
body, Aqwa first calculates the vertical shifting position of
the center of gravity to keep the displacement unchanged. Then, at
the body's new orientation and position state, the wetted body surface
can be determined numerically. Denoting the directional angle between
the horizontal hinge axis and the global X-axis as and the inclination angle about the hinge
axis from the initial equilibrium position as
, the new position of the center of gravity (X’g
, Y’g
, Z’g
) and the
corresponding wetted body surface as
, the righting moments about the horizontal axes
of GXYZ are
(3–16) |
where is the hydrostatic pressure.
The righting moments about the hinge axis and its perpendicular axis on the water plane are
(3–17) |
This can be can be further interpreted
into the conventional value used in the cross curves of stability
for a free-floating ship (see [40])
(3–18) |
where represents an arbitrary but fixed
pole above the center of gravity and parallel to the hinge axis, as
shown in Figure 3.2: Large Angle Stability.