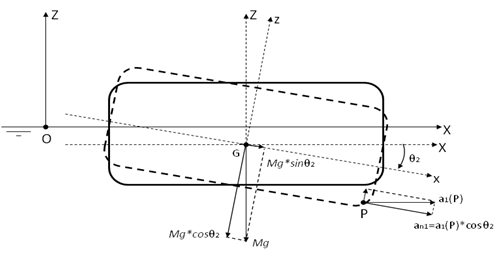
Effective nodal accelerations in the local structure axes (LSA)
can be calculated in Aqwa. As shown in Figure 14.1: Effective Surge Acceleration in LSA, the structure has a pitch motion RAO
of and a surge motion RAO of
, for a unit amplitude wave with frequency of
. The motion RAOs
and
are complex numbers.
Based on the assumption of small amplitude motion responses, the gravitational force in the local structure axes (LSA) can be approximated as
(14–1) |
Denoting as a nodal position in the local
structure axes, the nodal acceleration in the local structure x-axis
is
(14–2) |
The inertia force due to the local acceleration in the x-direction is
(14–3) |
Summing the above inertia force with the gravitational force in the local structure x-axis, the effective nodal acceleration in this local axis is defined as
(14–4) |
which can be simplified to:
(14–5) |
Similarly, the effective nodal acceleration RAO in the local structure y-axis is
(14–6) |
where , in which the sway and
roll motion RAOs
and
are complex numbers.
The effective roll acceleration is defined as
(14–7) |
where is the imaginary unit.
Based on the definitions in Equation 14–5 through Equation 14–7, the effective nodal x- (surge), y- (sway) and about x- (roll) velocity and motion RAOs in the local structure axes are defined as
(14–8) |