Benchmark C1

Overview

Reference:

S. Timoshenko, S, Woinowsky-Knieger, Theory of Plates and Shells, McGraw-Hill Book Co., Inc., New York, NY, 1959, pg. 202, Approximate Solution

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

3D 8-Node Structural Solid Elements (SOLID185)

3D 10-Node Tetrahedral Structural Solid Elements (SOLID187)

3D 20-Node Structural Solid Elements (SOLID186)

Input Listing:

vmc1.dat

Test Case

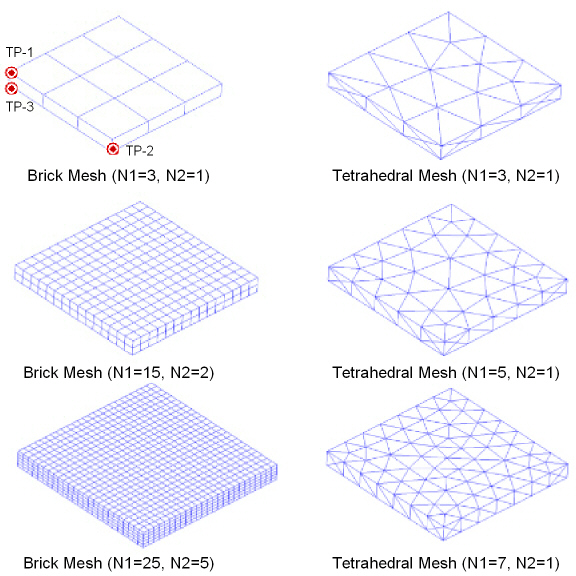
A rectangular plate with built-in edges is subjected to a uniform pressure load on the top and bottom surface. Monitor displacement and stress results at three target points for a series of mesh refinements for different elements. Compare the effect of increased mesh refinement on the percent energy error norm.

Figure 587: Built-in Plate Problem Sketch

Material Properties

Geometric Properties

Loading and Boundary Conditions for Mechanical APDL Model

E = 1 x 10⁷ psi

υ = 0.3

a = 10 in

t = 1 in

Parameter Definitions

N1 = no. elements along each horizontal edge

N2 = no. elements through thickness

Loading:

Pressure = 1000 psi

Boundary Conditions:

At X = a/2, UX = 0

At x = a/2 and Z = 0, UZ = 0

At Y = a/2, UY = 0

At Y = a/2 and Z = 0, UZ = 0

At X = 0, UX = 0

At Y = 0, UY = 0

At Z = 0, UX = UY = 0

At Z = -t/2, P = -500

Figure 588: Representative Mesh Options

Solution Information

Table 23: Target Solution

ETYP	N1	N2	DOF	% Error Norm	UZ(1), in	SX(2), ksi	SX(3), ksi
95	25	10	45708	10	-.0172	-32.124	14.465

Table 24: Results Comparison

ETYP	N1	N2	DOF	% Error Norm	UZ(1)^[a]	SX(2)^[a]	SX(3)^[a]
185	3	1	96	56.946	0.928	0.434	0.935
185	6	1	294	34.017	0.962	0.653	0.973
185	15	2	2304	19.154	0.980	0.850	0.991
185	20	4	6615	14.591	0.987	0.913	0.996
185	25	5	12168	13.202	0.990	0.936	0.997
186	3	1	288	8.365	0.958	0.829	1.037
186	6	1	945	7.725	0.978	0.955	1.006
186	15	2	8160	10.250	0.991	0.961	0.999
186	20	4	24507	10.160	0.997	1.001	1.000
187	3	1	741	37.573	0.957	0.822	0.977
187	5	1	1377	27.360	0.974	0.934	1.001
187	6	1	1917	25.354	0.977	0.949	1.000
187	10	2	4629	20.425	0.984	0.966	1.000

^[a]UZ(1), SX(2), and SX(3) show percentages normalized with Target Solution and have no units.

Table 25: Results Comparison - Shell Element and Analytical Solution

ETYP	N1	N2	DOF	% Error Norm	UZ(1), in	SX(2), ksi	SX(3), ksi
35	5	1	576	NA	-.0165	-29.580	14.303
Approximate Analytical Solution (neglecting shear deflection)					-.0138	-30.780	13.860

Assumptions, Modeling Notes, and Solution Comments

The problem exhibits symmetry about the midplane of the plate, and about the X and Y axes. This symmetry allows for a 1/8 symmetry sector to be modeled.
The approximate analytical solution neglects shear deflection. Shear deflection is accounted for in the finite element solutions.
The target solution is obtained from a fine mesh solution using SOLID186.
The 8-node isoparametric shell (SHELL281), subjected to the same loading, has results in line with the target solution. The SHELL281 element takes into account shear deflection effects.
Deflection and bending stresses converge quickly to the target solution at the center of the plate (target points 1 and 3) for the solid element test cases.
Bending-stresses are maximum at the built-in edges, peaking at the midspan of the plate (target point 2). It can be seen that a significant number of elements through the plate thickness are required to accurately predict the bending stresses at the built-in edge for the solid elements.
The percent error in energy norm remains relatively high as the mesh is refined, with most of the error energy located at the built-in edges. This behavior is expected at built-in edges where point-wise inaccuracies in the solution occur. The displacement and stress results for which the refinement was targeted are quite good, despite the high energy error.