VM90

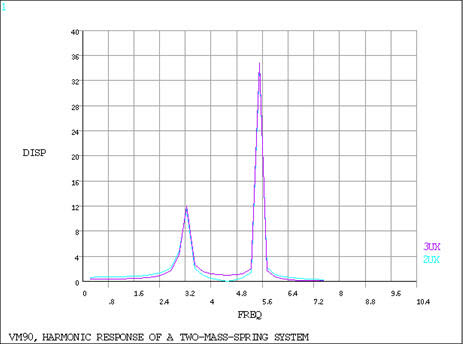
VM90
Harmonic Response of a Two-Mass-Spring System

Overview

Reference:W. T. Thomson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pg. 178, ex. 6.6-1.
Analysis Type(s):Harmonic Analysis (ANTYPE = 3)
Element Type(s):
Spring-Damper Elements (COMBIN14)
Structural Mass Elements (MASS21)
Input Listing:vm90.dat

Test Case

Determine the response amplitude (Xi) and phase angle (Φi) for each mass (mi) of the system in Figure 127: Two-Mass-Spring System Problem Sketch when excited by a harmonic force (F1sin ωt) acting on mass m1.

Figure 127: Two-Mass-Spring System Problem Sketch

Two-Mass-Spring System Problem Sketch

Material PropertiesLoading
m1 = m2 = 0.5 lb-sec2/in
k1 = k2 = kc = 200 lb/in
F1 = 200 lb

Analysis Assumptions and Modeling Notes

The spring lengths are arbitrarily selected and are used only to define the spring direction. A frequency range from zero to 7.5 Hz with a solution at 7.5/30 = 0.25 Hz intervals is chosen to give an adequate response curve. POST26 is used to get amplitude versus frequency display.

Results Comparison

TargetMechanical APDLRatio
X1 , in (f = 1.5 Hz)[1]0.822720.822721.000
Angle1, deg (f = 1.5 Hz)0.00000.0000-
X2 , in (f = 1.5 Hz)[1]0.462740.462741.000
Angle2, deg (f = 1.5 Hz)0.0000.0000-
X1 , in (f = 4.0 Hz)0.511450.511461.000
Angle1, deg (f = 4.0 Hz)180.00180.001.000
X2 , in (f = 4.0 Hz)1.21531.21531.000
Angle2, deg (f = 4.0 Hz)180.00180.001.000
X1 , in (f = 6.5 Hz)0.585130.585121.000
Angle1, deg (f = 6.5 Hz)180.00180.001.000
X2 , in (f = 6.5 Hz)0.269660.269651.000
Angle2, deg (f = 6.5 Hz)0.00000.0000-

  1. X1 = UX @ m1 (node 2) X2 = UX @ m2 (node 3)

Figure 128: Amplitude vs. Frequency

Amplitude vs. Frequency