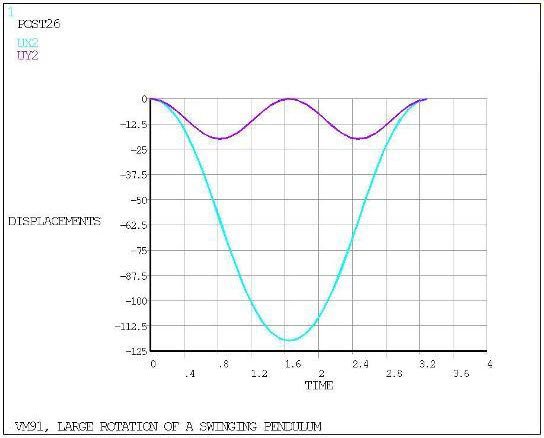
VM91
VM91
Large Rotation of a Swinging Pendulum
Test Case
A pendulum consists of a mass m supported by a rod of length
 and cross-sectional area A. Determine the motion
of the pendulum in terms of the displacement of the mass from its
initial position Θo in the x and
y directions, δx and δy, respectively. The pendulum starts with zero initial
velocity.
and cross-sectional area A. Determine the motion
of the pendulum in terms of the displacement of the mass from its
initial position Θo in the x and
y directions, δx and δy, respectively. The pendulum starts with zero initial
velocity.
Analysis Assumptions and Modeling Notes
A large deflection solution is required. An initial time step
is defined over a small time increment (.01/5 = .002 sec) to allow
an initial step change in acceleration to be attained. Subsequent
integration time steps (1.64142/8 = .205 sec) are based on
 1/24 of the period to allow the initial step change
in acceleration to be followed reasonably well.
1/24 of the period to allow the initial step change
in acceleration to be followed reasonably well.
Several load steps are defined for clearer comparison with theoretical
results. POST26 is used to process results from the solution phase.
and cross-sectional area A. Determine the motion
of the pendulum in terms of the displacement of the mass from its
initial position Θo in the x and
y directions, δx and δy, respectively. The pendulum starts with zero initial
velocity.
1/24 of the period to allow the initial step change
in acceleration to be followed reasonably well.