VM75
VM75
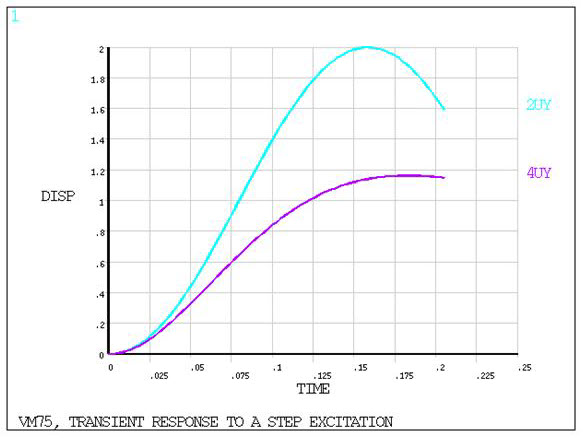
Transient Response to a Step Excitation
Test Case
A spring-mass-damping system, initially at rest, is subjected to a step force change F acting on the mass. Determine the maximum deflection umax for the undamped case. Determine the displacement u at time t for two damping ratios:
ξ = 0.0 (undamped)
ξ = 0.5
| Material Properties | Loading | ||||
|---|---|---|---|---|---|
|
|
Analysis Assumptions and Modeling Notes
The node locations are arbitrarily selected. The damping coefficient
c is calculated as 2ξ sqrt(km) = 0.0 and 10 lb-sec/in for ξ
= 0.0 and ξ = 0.5 respectively. A static solution is done at the
first load step. The maximum time of 0.205 sec allows the masses
to reach their largest deflections. The integration time step (0.0025
sec) is based on
1/120 of the period
to allow the initial step acceleration change to be followed reasonably
well and to produce sufficient printout for the theoretical comparison.
POST26 is used to get displacement versus time display.