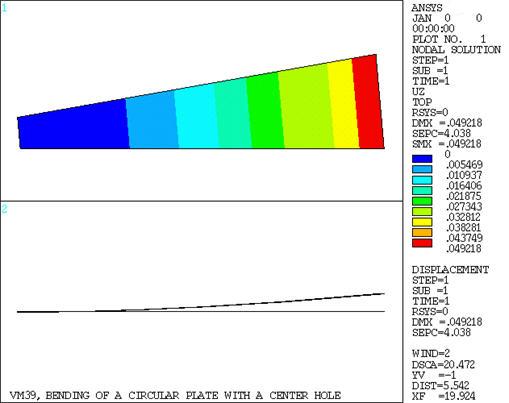
VM39
VM39
Bending of a Circular Plate with a Center Hole
Test Case
A circular plate of thickness t with a center hole is rigidly
attached along the inner edge and unsupported along the outer edge.
The plate is subjected to bending by a moment Ma applied uniformly along the outer edge. Determine the maximum deflection δ
and the maximum slope Φ of the plate. In addition, determine
the moment M and stress σx at the top
centroidal locations of element 1 (near inner edge) and element 6
(near outer edge).
Analysis Assumptions and Modeling Notes
Since the problem is axisymmetric only a small sector of elements
is needed. A small angle Θ = 10° is used for approximating
the circular boundary with a straight-edged element. A radial grid
with nonuniform (3:1) spacing is used. The calculated load is equally
divided and applied to the outer nodes.
The model is first solved using SHELL63 elements and then using SHELL181 elements.