VM40

VM40
Large Deflection and Rotation of a Beam Pinned at One End

Overview

Reference: Any basic mathematics book
Analysis Type(s): Nonlinear Transient Dynamic Analysis (ANTYPE = 4)
Element Type(s): 3D 2 Node Beam (BEAM188)
Input Listing: vm40.dat

Test Case

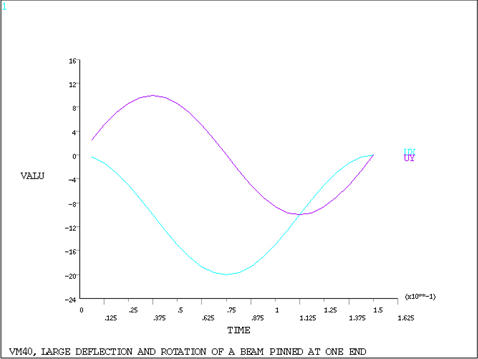
A massless beam of length L is initially at position AB on a horizontal frictionless table. Point A is pinned to the table and given a large rotation Θz through a full revolution at speed ωz. Determine the position of the beam in terms of δ, and Θ at various angular locations. Show that the beam has no axial stress σ at any position.

Figure 54: Beam Problem Sketch

Beam Problem Sketch

Material PropertiesGeometric PropertiesLoading
E = 30 x 106 psi
ρ = 1 x 10-10 lb-sec2/in4
L = 10 in
ωz = 400 rpm (ccw)

Analysis Assumptions and Modeling Notes

The beam area, moment of inertia, and thickness have no effect on the solution and are assumed equal to 1.0. Density (ρ) is assigned as nearly zero (1 x 10-10) to avoid centrifugal effects in the problem. Since this is rigid body motion, the time step is chosen to obtain the solution at discrete locations. The speed of 400 rpm is obtained by rotating one revolution in 0.15 sec (1/400th of a minute).

Results Comparison

Rotationz, degDeflection TargetMechanical APDLRatio
60Deflectionx (in)-5.0-5.01.00
90Deflectiony (in)10.010.01.00
180Deflectionx (in)-20.0-20.01.00
210Deflectiony (in)-5.0-5.01.00
315Deflectionx (in)-2.93-2.931.00
360Deflectiony (in)0.00.0-

Note:  Axial stress, σ 0, at each position.

Figure 55: Displacement of the Free End

Displacement of the Free End