VM311
VM311
Electrostatic-Structural Analysis of a Cylindrical Capacitor
Overview
| Reference: | Any basic Electrostatics textbook |
| Analysis Type(s): |
Static Analysis (ANTYPE = 0) Linear Perturbation Static Analysis (ANTYPE = 0) Linear Perturbation Modal Analysis (ANTYPE = 2) Linear Perturbation Harmonic Analysis (ANTYPE = 3) |
| Element Type(s): |
3D 20-Node Coupled-Field Solid (SOLID226) Spring-Damper (COMBIN14) Structural Mass (MASS21) |
| Input Listing: | vm311.dat |
Test Case
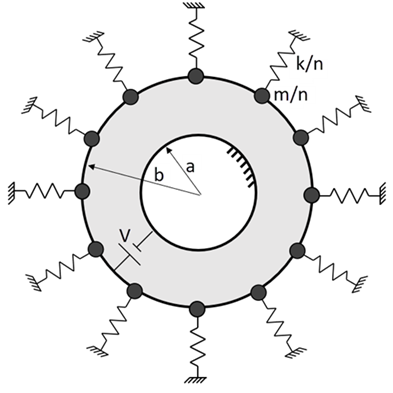
A capacitor made of two concentric conducting cylinders of radii a and b (a < b) has its inner cylinder fixed and the outer cylinder attached to an evenly distributed set of mass-springs as shown in the first problem sketch below. The space between the cylindrical electrodes is filled with air. A voltage differential is applied first between the conductors to determine the outer cylinder displacement until the pull-in voltage (VPI) is reached. Then the model is restarted from a selected bias voltage (VDC), and a series of linear perturbation analyses are performed to determine the static, modal, and harmonic responses of the DC-biased capacitor.
| Material Properties | Geometric Properties | Loading | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Free space permittivity:
Spring constant:
Plate mass:
|
Inner radius:
Outer radius:
Length (cylinder depth):
|
Static Analyses:
Linear Perturbation Analyses:
|
Analysis Assumptions and Modeling Notes
The space between the cylindrical electrodes is modeled using the electrostatic-structural analysis option (KEYOPT(1) = 1001) of SOLID226 to allow for the deformation of the air region induced by the electrostatic force acting between the electrodes. A negligible elastic modulus is assigned to this region. KEYOPT(4) is set to 1 to avoid applying the electrostatic forces to the interior nodes of the air region. The nodes of SOLID226 located on radius b are each attached to a spring modeled by the spring-damper element (COMBIN14). The stiffness of each spring is k/n where n is the total number of springs. Likewise, to account for the mass of the electrode, a point mass m/n is defined by structural mass (MASS21) at each node of radius b. The angular and axial components of displacement, UY and UZ, are all suppressed. The radial component UX is constrained to remain uniform on the outer cylinder while set to zero on the inner cylinder.
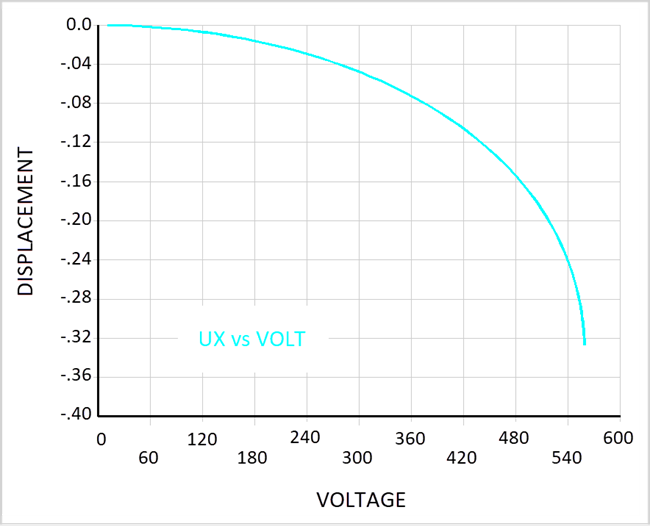
The analytical value for the pull-in voltage is 559.23 V. The nonlinear analysis runs until 559 V is reached. The test case is voltage-controlled, but the time steps are bisected based on the increments of displacement using CUTCONTROL,ULIMIT. This means convergence will be maintained as the pull-in voltage is approached. The displacement-voltage curve is shown in the graph below.
For a given value of displacement, the corresponding value of voltage is obtained from the analytical solution, and the ratio of numerical and analytical voltages averaged along the displacement-voltage curve is obtained by
where is the number of substeps.
Results Comparison
Nonlinear static analysis till pull-in voltage:
| Target | Mechanical APDL | Ratio | ||
| Disp-volt curve |
| — | — | 1.000067 |
| Capacitance at VDC |
| 0.863125E-04 | 0.86315E-04 | 1.000029 |
| Electrostatic force at VDC |
| 5.69337 | 5.69446 | 1.000191 |
Linear perturbation static analysis (voltage load):
| Target | Mechanical APDL | Ratio | ||
| Displacement |
where
| 0.0118528 | 0.0118937 | 1.003454 |
Linear perturbation static analysis (displacement load)
| Target | Mechanical APDL | Ratio | ||
| Voltage |
| 4.91669 | 4.91748 | 1.000162 |
Linear perturbation modal analysis (resonance)
| Target | Mechanical APDL | Ratio | ||
| Frequency |
| 109.965 | 109.784 | 0.998360 |
Linear perturbation modal analysis (anti-resonance):
| Target | Mechanical APDL | Ratio | ||
| Frequency |
where
| 120.171 | 120.010 | 0.998654 |
Linear perturbation harmonic analysis (actuator mode):
| Target | Mechanical APDL | Ratio | ||
| Displacement |
| 0.0149419 | 0.0150064 | 1.004315 |
Linear perturbation harmonic analysis (sensor mode):
| Target | Mechanical APDL | Ratio | ||
| Voltage |
| -9.03894 | -9.06992 | 1.003427 |