VM309

Overview

Reference:	S.P. Timoshenko & J.M. Gere. (1961). Theory of Elastic Stability (2nd ed.). (229). New York, NY: McGraw-Hill.
Analysis Type(s):	Buckling (ANTYPE = 1)
Element Type(s):	3D 3-Node Beam (BEAM189)
Input Listing:	vm309.dat

Test Case

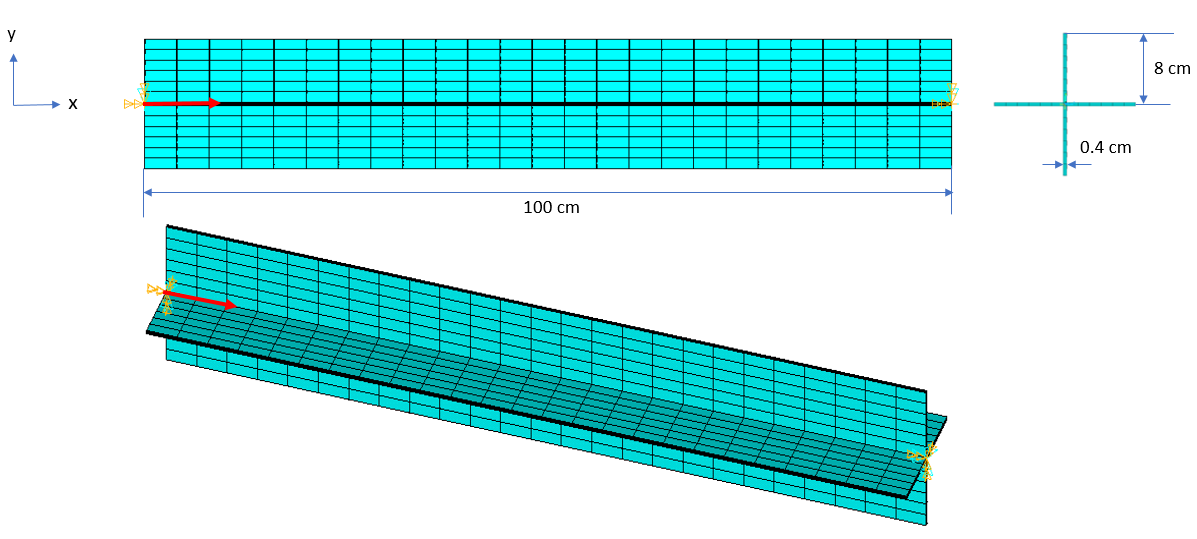
The beam is a cruciform section with four identical flanges of length 'l', width 'b' and thickness 't.' All the displacements and rotations at both ends of the beam are fixed, except for the x-displacement degrees of freedom where the axial force is applied. The warping degrees of freedom are activated but not constrained. Determine the critical buckling load for the first three modes.

Figure 561: Initial Boundary Conditions

Material Properties	Geometric Properties	Loading
E = 21000 kN/cm² G = 8077 kN/cm²	Length, l = 100 cm Width, b = 8 cm Thickness, t = 0.4 cm Area = 12.64 cm² Polar moment of Inertia = 273.24 cm⁴ Warping Constant = 3.6297 cm⁶ Torsional Constant = 0.69134 cm⁴	F = 1 N at l = 0

Material Properties

Geometric Properties

Loading

E = 21000 kN/cm²

G = 8077 kN/cm²

Length, l = 100 cm

Width, b = 8 cm

Thickness, t = 0.4 cm

Area = 12.64 cm²

Polar moment of Inertia = 273.24 cm⁴

Warping Constant = 3.6297 cm⁶

Torsional Constant = 0.69134 cm⁴

F = 1 N at l = 0

Analysis Assumptions and Modeling Notes

The linear buckling analysis is solved using the PSTRES command. Doubly symmetric cross-section is used to demonstrate how an axial compressive load may cause purely torsional buckling.

Results Comparison

Critical Buckling Load (kN)
Modes	Target	Mechanical APDL	Ratio
1	261.792	261.798	1.000
2	272.232	272.237	1.000
3	289.633	289.632	1.000