VM299

Overview

Reference:

Alexis Billon et al., “Introducing Atmospheric Attenuation Within a Diffusion Model for Room-Acoustic Predictions,” 4040-4043, Journal of the Acoustical Society of America, 123(6), June 2008.

Analysis Type(s):

Static (ANTYPE = 0)

Element Type(s):

3D 20-Node Acoustic Solid (FLUID220)

Input Listing:

vm299.dat

Test Case

Sound diffusion is modeled in a flat room of size 30 × 30 × 3 m³. A sound source is placed at (2,2,1) with a sound power level of 1 × 10^-2 W. The wall absorption coefficient is equal to 0.1. The coefficient of atmospheric attenuation is 0.01 m^-1.

Figure 535: Finite Element Model of a Flat Room

Material Properties

Geometric Properties

Loading

Speed of sound c₀ = 343 m/s

Density ρ= 1.21 kg/m³

Wall absorption coefficient α = 0.1

Atmospheric attenuation coefficient attn. = 0.01 m^-1

Room length = 30 m

Room width = 30 m

Room height = 3 m

Sound power source = 1 × 10^-2 W

Analysis Assumptions and Modeling Notes

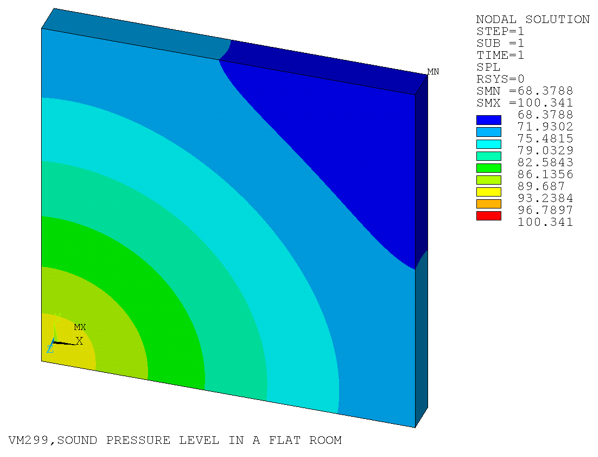
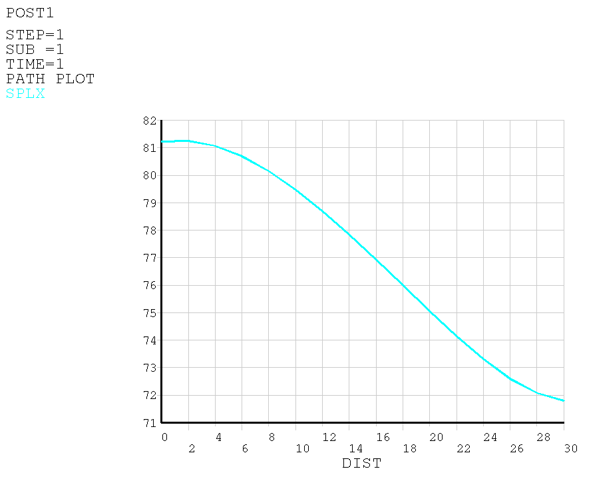
Steady-state analysis is performed to determine the sound pressure level inside the room. In the post-processing, the sound pressure level (SPL) is listed every 2 m along a line passing through the room center at 1 m high. The sound pressure level is calculated in Mechanical APDL as:

SPL = 10 × log₁₀((ρ × c₀² × w) / P_ref²)

where w is diffuse sound energy and reference pressure P_ref = 2 × 10^-5. Variation of SPL inside the room and along the selected line is plotted in Figure 536: Sound Pressure Level in the Flat Room and Figure 537: Sound Pressure Level Along the Selected Line.

Results Comparison

SPL at Position	Target	Mechanical APDL	Ratio
X = 5 m	80.0	80.906	1.011
X = 10 m	79.0	79.479	1.006
X = 15 m	77.5	77.394	0.999
X = 20 m	76.0	75.057	0.988
X = 25 m	74.5	72.936	0.979

Figure 536: Sound Pressure Level in the Flat Room

Figure 537: Sound Pressure Level Along the Selected Line