VM252

VM252
Gurson Bar-Necking Benchmark with Applied Displacement - 2D Analysis

Overview

Reference:

N. Aravas, "On the Numerical Integration of a Class of Pressure Dependent Plasticity Models", International Journal for Numerical Methods in Engineering, Vol. 24, pp. 1395-1416, Section 5.3, Figure 10 (1987).

Analysis Type(s):

Static analysis (ANTYPE = 0)

Element Type(s):

2D 4-Node Structural Plane Elements (PLANE182)

2D 8-Node Structural Plane Elements (PLANE183)

Input Listing:

vm252.dat

Test Case

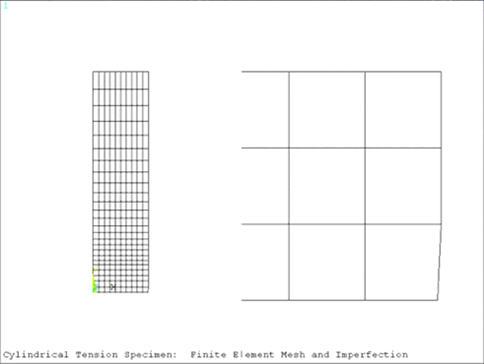
The model represents the necking of an axisymmetric specimen. The initial radius of the specimen was described to be 1" and the length was set to four times the initial radius. A slight imperfection is found at the bottom of the model to create the initial notch, which is offset by 0.005*R_o. For clarification, the finite element mesh and the geometric imperfection are found in Figure 428: Representative Finite Element Model. To initiate growth of the notch, a displacement in the y-direction was applied to the top of the model that was set to 0.7602".

Figure 428: Representative Finite Element Model

Material Properties

Gurson Material Model

Elastic Material Model

E = 1000000 lb/in²

ν = 0.30

Geometric Properties

L = 1

T = 0.02

q₁ = 1.5

q₂ = 1.0

q₃ = q₁²

ε_n = 0.3

f_o = 1E-8

f_n = 0.04

s_n = 0.1

ε_n = 0.3

σ_y = E/300.0

n = 0.1

Loading

U_app = 0.7602" @ y = 4"

U_x = 0 @ x = 0"

U_y = 0 @ y = 0"

Analysis Assumptions and Modeling Notes

A 2D analysis is performed with both PLANE182 and PLANE183 elements. Two material models are introduced into the model, an elastic and Gurson model. The elastic model is based upon a power law and is presented for hardening purposes. The coefficients for input were taken from the reference provided.

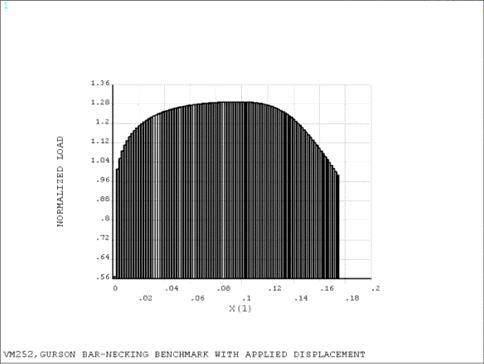
Due to the nonlinear behavior and complexity of the problem, it is suggested to first increase the number of substeps within the solution module until convergence is reached or perform mesh refinement. Within the provided input listing, the total force along y = 4.0" is recorded and plotted against x, where x is defined by the following relationship: x = log(1+ dispY/L_o).

Graphical Results Comparison

Figure 429: Material Behavior of Specimen

Numerical Results Comparison

	Target	Mechanical APDL	Ratio
Results using PLANE182 Elements	1.25	1.2895	0.969
Results using PLANE183 Elements	1.25	1.2896	0.969