VM220

VM220
Electromigration Diffusion Problem with Perfectly Blocking Diffusion Barrier

Overview

Reference:

Clement, J.J., Lloyd, J.R., "Numerical Investigation of the Electromigration Boundary Value Problem", Journal of Applied Physics 71(4), 15 February 1992, pp. 1729-1731

Analysis Type(s):

Transient Analysis (ANTYPE = 4)

Element Type(s):

2D 8-Node Diffusion Elements (PLANE238)

2D 8-Node Coupled-Field Elements (PLANE223)

Input Listing:

vm220.dat

Test Case

Diffusion and mass transport effects due to electromigration are considered in a rectangular conductor of length L and height H. A concentration load of C0 is applied at one end of the plate (x = -L) and a zero diffusion flux boudary condition (blocking diffusion barrier) is applied at the other end (x = 0) of the plate. A transient analysis is performed to determine the concentration evolution at the blocking diffusion end of the plate.

Figure 359: Problem Sketch

Material Properties

Geometric Properties

Pure Diffusion Element (PLANE238)

Diffusivity coefficient = 1 m²/s

(MP,DXX)

Coupled Electric-Diffusion Element (PLANE223)

Diffusivity coefficient = 1 m²/s

(MP,DXX)

Electrical resistivity = 1 x 10^-7 Ohm-m

(MP,RSVX)

Effective charge/Boltzmann constant = 1.16045 x 10⁴ C-K/J

(TB,MIGR)

Length, L = 2 m

Height, H = 0.2 m

PLANE238

Concentration at x = -L, C0 = 1

Transport velocity, D*ALPHA = 1 m/s

(BF,,VELO)

PLANE223

Concentration at x = -L, C0 = 1

Voltage load, V0 = 0.8152 x 10^-1 V

Temperature = 200 °C

(BF,,TEMP)

Offset temperature = 273 °C

(TOFFST)

Analysis Assumptions and Modeling Notes

Two approaches are used to solve this boundary value problem. The first solution uses a diffusion element type (PLANE238) and applies the electromigration driving force ALPHA as transport velocity body load (BF, VELO). The second approach uses a coupled electric-diffusion element type (PLANE223 with KEYOPT(1) = 100100) in conjunction with a Migration Model (TB,MIGR). The Migration Model is used to define the effective electric charge Z*e, which determines the direction and magnitude of the electron-atom momentum exchange responsible for the mass transport of atoms due to the electric current. The voltage DOFs are constrained at location x = 0 and a voltage load of V0 is applied at node 1 in order to achieve the desired electromigration driving force ALPHA.

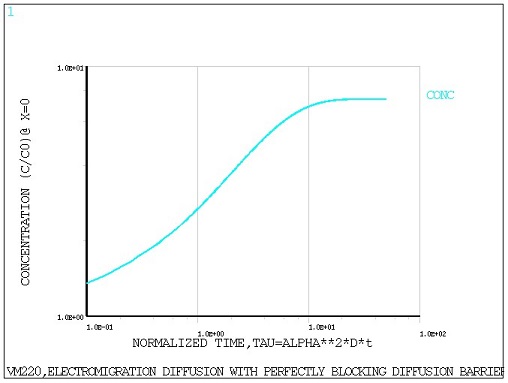
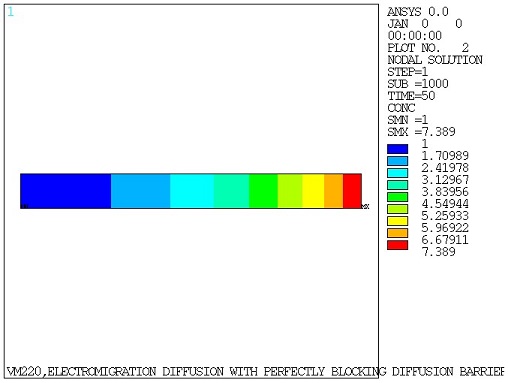
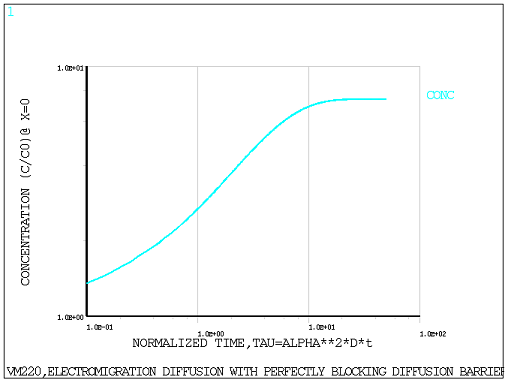
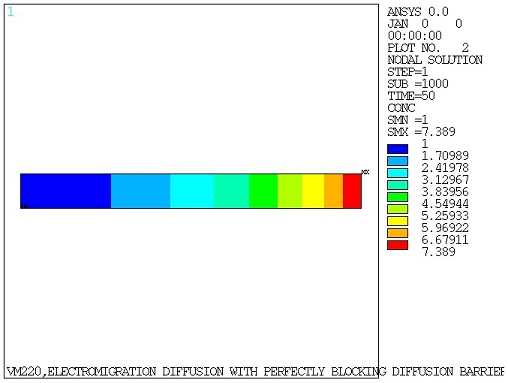
Transient diffusion and electric-diffusion analyses with stepped loading (KCB,1) are performed with an end time = 50 seconds and a time increment of 0.05 seconds to determine the concentration at the blocking boundary x = 0 for all time points. Initial concentration C0 = 1 is imposed using the IC command. The obtained results are then compared against the reference solution (Figure 1, C (-L, t) = C0, alpha*L = 2).

Results Comparison

The calculated concentration is compared to the target results at the blocking boundary (x = 0) for several normalized time points.

Normalized Time	Target	Mechanical APDL	Ratio
Concentration values using PLANE238 elements
0.01	1.11	1.25	1.13
1	2.70	2.71	1.00
10	6.69	6.89	1.03
39.5	7.35	7.39	0.99
Concentration values using PLANE223 elements
0.01	1.11	1.17	1.05
1	2.70	2.69	0.99
10	6.69	6.89	1.03
39.5	7.35	7.39	0.99

The calculated concentration at the blocking barrier (x = 0) as a function of normalized time is shown in the following figures for PLANE238 and PLANE223 elements respectively.

Figure 360: Concentration vs. Normalized Time using PLANE238 Elements

Figure 361: Nodal Concentration Plot at Time = 50 seconds using PLANE238 Elements

Figure 362: Concentration vs. Normalized Time using PLANE223 Elements

Figure 363: Nodal Concentration Plot at Time = 50 seconds using PLANE223 Elements