VM168
VM168
Magnetic Field in a Nonferrous Solenoid
Test Case
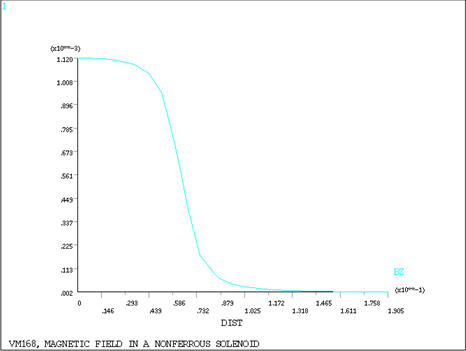
A nonferrous solenoid is wound with one layer of No. 26 enameled wire and carries a current I. Determine the magnetic flux density on the centerline at
the center of the coil
the end of the coil
at a point 5 inches from the end of the coil
| Geometric Properties | Loading | ||||||
|---|---|---|---|---|---|---|---|
|
|
Analysis Assumptions and Modeling Notes
The number of turns is N = s/d = 5/.0216 = 231. Therefore, N x I = 115.5 Ampere-turns. Since no ferromagnetic materials are present, the field due to induced magnetization, Hm = 0, and thus no scalar potential is required. The total field can be determined from the numerical integration of the coil source field upon specification of the coil with the current source element (SOURC36). Since the field is symmetric, an arbitrary arc of 10° is chosen with an additional symmetry plane taken along the coil midspan. A sufficient number of integration points (50) are chosen along the Z-axis to adequately represent the coil. Only one point is specified through the coil thickness. The Reduced Scalar Potential (RSP) is selected since only a source field is to be calculated.