VM105
VM105
Heat Generating Coil with Temperature Conductivity
Test Case
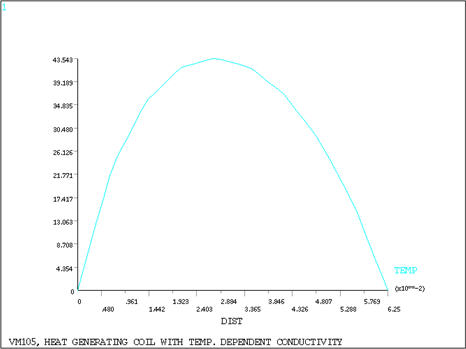
A long hollow generator coil has its inner and outer surface
temperatures maintained at temperature To while
generating Joule heat at a uniform rate
. The thermal conductivity of the coil material varies
with temperature according to the function k(T) = C0 + C1 T. Determine the temperature distribution
in the coil.
| Material Properties | Geometric Properties | Loading |
|---|---|---|
|
C0 = 10 Btu/hr-ft-°F C1 = 0.075 Btu/hr-ft-°F2 |
ri = 1/4 in = 1/48 ft ro = 1 in = 1/12 ft |
To = 0°F
|
Analysis Assumptions and Modeling Notes
Since the problem is axisymmetric only a symmetry sector (one-element wide) is needed. A small angle (Θ=10°) is used for approximating the circular boundary with a straight-sided element. Adiabatic boundary conditions are assumed at the symmetry edges. The steady-state convergence procedures are used. Note that this problem can also be modeled using the axisymmetric option as in VM102 .