Either the total nodal pressure or the scattered nodal pressure is solved and output at the nodes. Using the calculated nodal pressure values, the pressure gradient is evaluated at the nodes and the element centroid, which is expressed as follows:

(8–181)

Both the nodal velocity (output as PG on the PRNSOL, PLNSOL, and PLVECT commands) and the element centroid velocity (output as SMISC on the element table) are calculated for modal (ANTYPE,MODAL) and full harmonic (ANTYPE,HARM) analyses as follows:

(8–182)

The nodal and element centroid sound pressure levels (SPL) are output in the post-processor. SPL is given by:

(8–183)

where:

(input as PREF on the R command, defaults to 20 x 10-6Pa)

In the frequency domain, the time-average root mean square quantities are calculated over one period of the sinusoidal function. In the time domain, the time-average root mean square quantities are calculated over the time increment .

The A-weighted sound pressure level (dBA) in the frequency domain is defined by:

(8–184)

where:

In room acoustics, the sound pressure level (SPL) is defined as:

(8–185)

where:

= acoustic energy density

ρ = mass density of fluid

c = speed of sound

The sound intensity is cast by both pressure and velocity:

(8–186)

In the frequency domain, the time-average sound intensity is given by:

(8–187)

where:

p = complex pressure

= complex conjugate velocity

The far-field pressure parameters (output via the PLFAR and PRFAR command) outside of the model are expressed as:

(8–188)

where:

= enclosed equivalent source surface (defined as MXWF on SF command).

= Green's function in radiation space (defaults to free space). It is defined as follows for the 3D and 2D cases, respectively:

(8–189)

(8–190)

= far-field observation position

= equivalent source position on the enclosed surface

k = wave number (k is equal to zero for an incompressible fluid)

H0(2) = zeroth order Hankel function of second kind

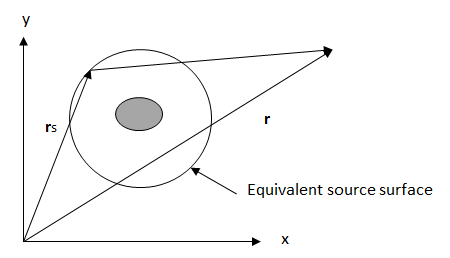
The Rayleigh integral predicts the radiated far-field pressure from a vibrating panel with an infinite baffle:

(8–191)

where:

= fluid density

= angular velocity

= normal displacement

Figure 8.2: Equivalent Source Principle

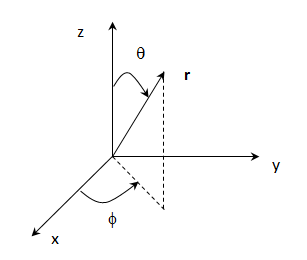
All acoustic far-field parameters are evaluated in the global spherical coordinate system shown in the following figure:

Figure 8.3: Spherical Coordinates

The sound power level radiated by the sound source is expressed as:

(8–192)

where:

The radiated sound power is expressed as:

(8–193)

The directivity of the sound source is expressed as:

(8–194)

where:

The directivity of the sound source is also expressed as:

(8–195)

The target strength (TS) is used to describe the reflected acoustic signals. Target strength is given by:

(8–196)

where:

The time-averaged sound power through an area S in a harmonic analysis is defined by:

(8–197)

In a network, the return loss and transmission loss are respectively defined as:

(8–198)

(8–199)

where:

The sound power parameters are output via the PRFAR, PLFAR, PRAS or PLAS command.

The acoustic surface quantities on the selected surface are defined as follows (and are output via the PRAS and PLAS commands):

where:

= pressure on the surface

= normal component of velocity on the surface

= surface area

The acoustic volumetric quantities on the selected elements are defined as follows (output by the PRAS and PLAS commands).

Acoustic time-averaged potential energy:

(8–200)

Acoustic time-averaged kinetic energy:

(8–201)

Average square of the L2 norm of pressure:

(8–202)

where:

= root mean square of acoustic pressure

= speed of sound

= mass density

= root mean square of particle velocity

If the frequency range is equally divided into segments and the pressures are calculated at the center of the frequency segment , the sound pressure level (SPL) of the frequency range is defined as follows (and output via the PRAS and PLAS commands):

(8–203)

where:

= SPL of frequency segment .

The A-weighted SPL of the frequency range is written as:

(8–204)

The equivalent radiated power (ERP) that estimates the radiated structure-borne sound power from the vibrating structural surface is defined as follows:

(8–205)

where:

= speed of sound

= mass density

= radiation factor

= normal velocity of vibrating structural surface