11.9. 3D Solids

This section contains shape functions for 3D solid elements. These elements are available in a number of configurations, including certain combinations of the following features:

Element shapes may be tetrahedra, pyramids, wedges, or bricks (hexahedra).
- If wedges or bricks, with or without extra shape functions (ESF)
With or without rotational degrees of freedom (RDOF)
With or without midside nodes

The wedge elements with midside nodes (15-node wedges) are either a condensation of the 20-node brick element or are based on wedge shape functions.

11.9.1. 4-Node Tetrahedra

These shape functions are either a direct 4-node tetrahedral such as SOLID285 or a condensation of an 8-node brick element such as SOLID5, FLUID30, or SOLID98.

Figure 11.10: 3D Solid Elements

The resulting effective shape functions are:

(11–175)

(11–176)

(11–177)

(11–178)

(11–179)

(11–180)

(11–181)

(11–182)

(11–183)

(11–184)

(11–185)

(11–186)

11.9.2. 10-Node Tetrahedra

These shape functions are for 10-node tetrahedron elements such as SOLID98 and SOLID227, or by condensation for SOLID90.

Figure 11.11: 10-Node Tetrahedra Element

(11–187)

(11–188)

(11–189)

(11–190)

(11–191)

(11–192)

(11–193)

11.9.3. 5-Node Pyramids

This element is a condensation of an 8-node brick element.

Figure 11.12: 8-Node Brick Element

The resulting effective shape functions are:

(11–194)

11.9.4. 13-Node Pyramids

These shape functions are for 13-node pyramid elements which are based on a condensation of a 20-node brick element:

Figure 11.13: 13-Node Pyramid Element

(11–195)

(11–196)

(11–197)

(11–198)

(11–199)

(11–200)

11.9.5. 6-Node Wedges Without ESF

Figure 11.14: 6-Node Wedge Element

The 6-node wedge elements are a condensation of an 8-node brick such as SOLID5 or FLUID30. These shape functions are for 6-node wedge elements without extra shape functions:

(11–201)

(11–202)

(11–203)

(11–204)

(11–205)

(11–206)

(11–207)

11.9.6. 6-Node Wedges With ESF

The 6-node wedge elements are a condensation of an 8-node brick such as SOLID5. (See Figure 11.14: 6-Node Wedge Element.) These shape functions are for 6-node wedge elements with extra shape functions:

(11–208)

(11–209)

(11–210)

11.9.7. 15-Node Wedges

These shape functions are for 15-node wedge elements such as SOLID90 that are based on a condensation of a 20-node brick element Equation 11–236. or are computed directly.

Figure 11.15: 15-Node Wedge Element

Elements in a wedge configuration use shape functions based on triangular coordinates and the r coordinate going from -1.0 to +1.0.

(11–211)

(11–212)

(11–213)

(11–214)

(11–215)

(11–216)

11.9.8. 8-Node Bricks Without ESF

Figure 11.16: 8-Node Brick Element

These shape functions are for 8-node brick elements without extra shape functions such as SOLID5 with KEYOPT(3) = 1, FLUID30, or SOLID225 with KEYOPT(11) = 0:

(11–217)

(11–218)

(11–219)

(11–220)

(11–221)

(11–222)

(11–223)

(11–224)

(11–225)

(11–226)

(11–227)

(11–228)

(11–229)

(11–230)

(11–231)

(11–232)

11.9.9. 8-Node Bricks With ESF

(Please see Figure 11.16: 8-Node Brick Element) These shape functions are for 8-node brick elements with extra shape functions such as SOLID5 with KEYOPT(3) = 0:

(11–233)

(11–234)

(11–235)

11.9.10. 20-Node Bricks

Figure 11.17: 20-Node Brick Element

These shape functions are used for 20-node solid elements such as SOLID90:

(11–236)

(11–237)

(11–238)

(11–239)

(11–240)

(11–241)

(11–242)

11.9.11. 8-Node Infinite Bricks

Figure 11.18: 3D 8-Node Brick Element

These shape functions and mapping functions are for the 3D 8-node solid brick infinite elements such as INFIN111:

11.9.11.1. Shape Functions

(11–243)

(11–244)

(11–245)

(11–246)

(11–247)

(11–248)

(11–249)

(11–250)

11.9.11.2. Mapping Functions

(11–251)

(11–252)

(11–253)

(11–254)

11.9.12. 20-Node Infinite Bricks

Figure 11.19: 20-Node Solid Brick Infinite Element

These shape functions and mapping functions are for the 3D 20-node solid brick infinite elements such as INFIN111:

11.9.12.1. Shape Functions

(11–255)

(11–256)

(11–257)

(11–258)

(11–259)

(11–260)

(11–261)

(11–262)

(11–263)

11.9.12.2. Mapping Functions

(11–264)

(11–265)

(11–266)

The shape and mapping functions for the nodes U, V, W, X, Y, Z, A, and B are deliberately set to zero.

11.9.13. General Axisymmetric Solids

This section contains shape functions for general axisymmetric solid elements. These elements are available in a number of configurations, including certain combinations of the following features:

A quadrilateral, or a degenerated triangle shape to simulate an irregular area, on the master plane (the plane on which the quadrilaterals or triangles are defined)
With or without midside nodes
A varying number of node planes (N_np) in the circumferential direction (defined via KEYOPT(2))

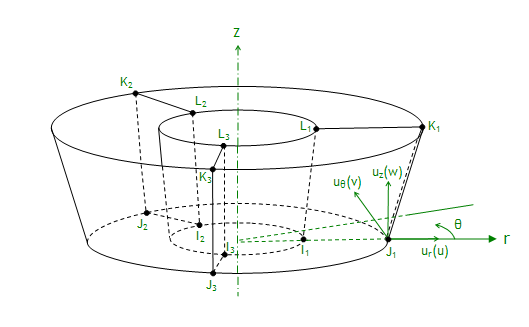
The elemental coordinates are cylindrical coordinates and displacements are defined and interpolated in that coordinate system, as shown in Figure 11.20: General Axisymmetric Solid Elements (when N_np = 3).

Figure 11.20: General Axisymmetric Solid Elements (when N_np = 3)

When N_np is an odd number (except , the interpolation function used for displacement is:

(11–267)

where:

i = r, θ, z

h_i (s, t) = regular Lagrangian polynominal interpolation functions like Equation 11–122 or Equation 11–137.

= coefficients for the Fourier terms.

When N_np is an even number other than 4, the interpolation function is:

(11–268)

When N_np = 4, the interpolation function is:

(11–269)

The temperatures are interpolated by Lagrangian polynominal interpolations in s, t plane, and linearly interpolated with θ in circumferential (θ) direction as:

(11–270)

where:

= node plane number in circumferential direction

T_n = same as Equation 11–130 and Equation 11–141.

11.9.13.1. General Axisymmetric Solid With 4 Base Nodes

All of the coefficients in Equation 11–267 and Equation 11–268 can be expressed by node displacements. Using u_r = u, u_j = v, u_z = w, and take N_np = 3 as an example.