The unstable mode predictions for the brake disc-pad assembly using all three methods were very close due to the relatively small prestress load. The linear non-prestressed modal solution predicted unstable modes at 6474 Hz, while the other two solution methods predicted unstable modes at 6470 Hz.
The mode shape plots for the unstable modes suggest that the bending mode of the pads and disc have similar characteristics. These bending modes couple due to friction, and produce a squealing noise.
Figure 1.5: Mode Shape for Unstable Mode (Mode 21) Obtained from the Linear Non-prestressed Modal Solution
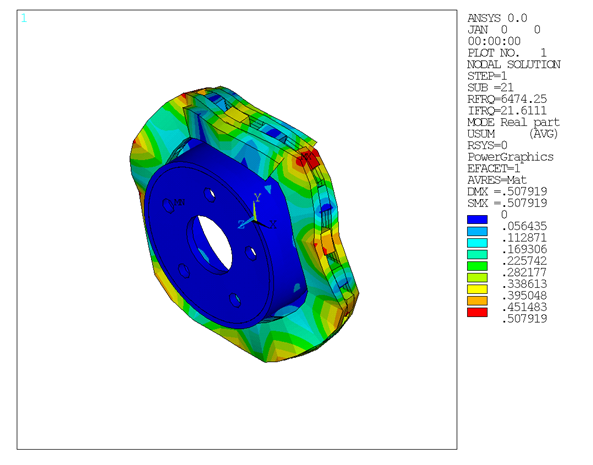
Figure 1.6: Mode Shape for Unstable Mode (Mode 22) Obtained from the Linear Non-prestressed Modal Solution
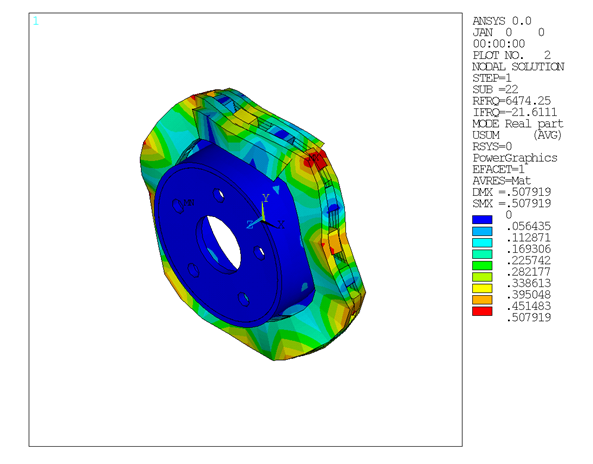
Table 1.1: Solution Output
| Linear non-prestressed modal | Partial nonlinear perturbed modal | Full nonlinear perturbed modal | ||||
|---|---|---|---|---|---|---|
| Mode | Imaginary | Real | Imaginary | Real | Imaginary | Real |
| 1.00 | 775.91 | 0.00 | 775.73 | 0.00 | 775.73 | 0.00 |
| 2.00 | 863.54 | 0.00 | 863.45 | 0.00 | 863.45 | 0.00 |
| 3.00 | 1097.18 | 0.00 | 1097.03 | 0.00 | 1097.03 | 0.00 |
| 4.00 | 1311.54 | 0.00 | 1311.06 | 0.00 | 1311.06 | 0.00 |
| 5.00 | 1328.73 | 0.00 | 1328.07 | 0.00 | 1328.07 | 0.00 |
| 6.00 | 1600.95 | 0.00 | 1600.66 | 0.00 | 1600.66 | 0.00 |
| 7.00 | 1616.15 | 0.00 | 1615.87 | 0.00 | 1615.87 | 0.00 |
| 8.00 | 1910.50 | 0.00 | 1910.50 | 0.00 | 1910.50 | 0.00 |
| 9.00 | 2070.73 | 0.00 | 2070.44 | 0.00 | 2070.44 | 0.00 |
| 10.00 | 2081.26 | 0.00 | 2080.98 | 0.00 | 2080.98 | 0.00 |
| 11.00 | 2676.71 | 0.00 | 2675.23 | 0.00 | 2675.23 | 0.00 |
| 12.00 | 2724.05 | 0.00 | 2722.61 | 0.00 | 2722.61 | 0.00 |
| 13.00 | 3373.96 | 0.00 | 3373.32 | 0.00 | 3373.32 | 0.00 |
| 14.00 | 4141.64 | 0.00 | 4141.45 | 0.00 | 4141.45 | 0.00 |
| 15.00 | 4145.16 | 0.00 | 4145.04 | 0.00 | 4145.04 | 0.00 |
| 16.00 | 4433.91 | 0.00 | 4431.08 | 0.00 | 4431.08 | 0.00 |
| 17.00 | 4486.50 | 0.00 | 4484.00 | 0.00 | 4484.00 | 0.00 |
| 18.00 | 4668.51 | 0.00 | 4667.62 | 0.00 | 4667.62 | 0.00 |
| 19.00 | 4767.54 | 0.00 | 4766.95 | 0.00 | 4766.95 | 0.00 |
| 20.00 | 5241.61 | 0.00 | 5241.38 | 0.00 | 5241.38 | 0.00 |
| 21.00 | 6474.25 | 21.61 | 6470.24 | 21.90 | 6470.24 | 21.90 |
| 22.00 | 6474.25 | -21.61 | 6470.24 | -21.90 | 6470.24 | -21.90 |
| 23.00 | 6763.36 | 0.00 | 6763.19 | 0.00 | 6763.19 | 0.00 |
| 24.00 | 6765.62 | 0.00 | 6765.51 | 0.00 | 6765.51 | 0.00 |
| 25.00 | 6920.64 | 0.00 | 6919.64 | 0.00 | 6919.64 | 0.00 |
| 26.00 | 6929.25 | 0.00 | 6929.19 | 0.00 | 6929.19 | 0.00 |
| 27.00 | 7069.69 | 0.00 | 7066.72 | 0.00 | 7066.72 | 0.00 |
| 28.00 | 7243.80 | 0.00 | 7242.71 | 0.00 | 7242.71 | 0.00 |
| 29.00 | 8498.41 | 0.00 | 8493.08 | 0.00 | 8493.08 | 0.00 |
| 30.00 | 8623.76 | 0.00 | 8616.68 | 0.00 | 8616.68 | 0.00 |
It is important to determine the modal behavior of individual components (disc and pads) when predicting brake-squeal noise. A modal analysis performed on the free pad and free disc model gives insight into potential coupling modes. The natural frequency and mode shapes of brake pads and disc can also be used to define the type of squeal noise that may occur in a braking system. Bending modes of pads and disc are more significant than twisting modes because they eventually couple to produce squeal noise.
An examination of the results obtained from the modal analysis of a free disc and pad shows that the second bending mode of the pad and ninth bending mode of the disc can couple to create dynamic instability in the system. These pad and disc bending modes can couple to produce an intermediate lock, resulting in a squeal noise at a frequency close to 6470 Hz.
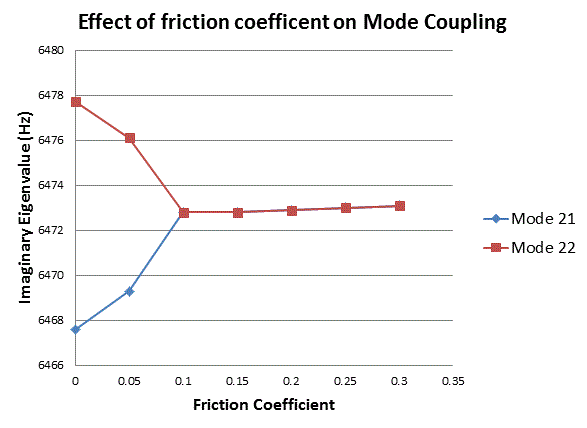
A parametric study was performed on the brake disc model using a linear non-prestressed modal solution with an increasing coefficient of friction. QRDAMP eigensolver is used to perform the parametric studies by reusing the symmetric real modes (QRDOPT,ON) obtained in the first load step.
The following plot suggests that modes with similar characteristics approach each other and couple as the coefficient of friction increases: