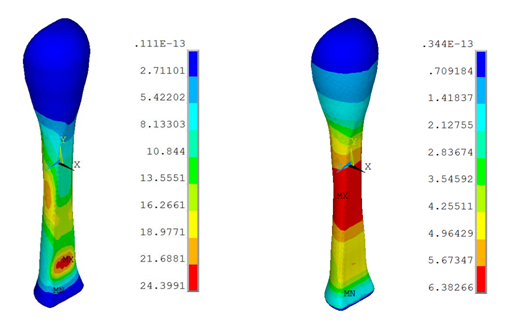
Because the ACL transmits tensile forces, experimental studies of this tissue are generally performed in uniaxial tension. The following figure shows the von Mises stress distribution for the ACL under the uniaxial tension at constant strain rate of 50 percent per second for anisotropic visco-hyperelastic and Neo-Hookean viscoelastic models:

Figure 32.3: Von Mises Stress (Anisotropic Visco-Hyperelastic and Neo-Hookean Viscoelastic)

In the anisotropic visco-hyperelastic model, the peak stresses in the ACL are seen near the insertion sites, suggesting that this area could be susceptible to injury.

Ligaments are highly anisotropic due to their fibrous structure.[7] The collagen fibers in the cruciate ligaments of the knee are highly aligned with the long axis; therefore, an anisotropic model is required to show the behavior of the ACL under deformation.

The strain rate during injury is a significant factor in determining the magnitude of the lesion. The stress-strain behavior of the ligament is therefore essential in order to examine the importance of the strain rates during the ACL movement.

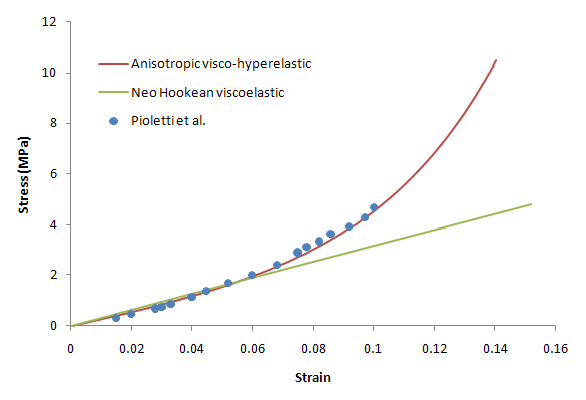
The following figure shows the stress-strain behavior of the ACL under uniaxial tension for visco-anisotropic, visco-hyperelastic, and Neo-Hookean viscoelastic material models along with the experimental results of Pioletti et al.[3]:

Figure 32.4: ACL Stress-Strain Plot

The stress and strain values are the average values on the cross-sectional area of the ACL.

The anisotropic visco-hyperelastic ACL model used in this problem exhibits a response closer to the experimental data when the ACL is subjected to uniaxial loading.

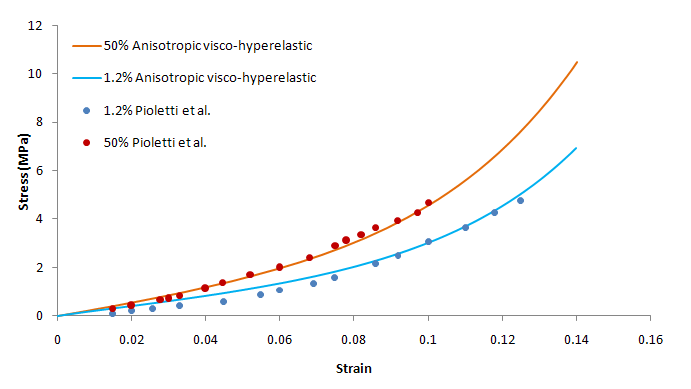
The following figure shows the stress- strain behavior of the ACL under uniaxial tension for the anisotropic visco-hyperelastic model with differing strain rates:

Figure 32.5: Stress-Strain at Differing Strain Rates

At high strain rates, the results are closer to the experimental results. It is known that damage in mature ligaments typically occurs at high load rates. The variation of ligament stress-strain behavior with strain rate is an indicator of the viscoelastic nature of the tissue.

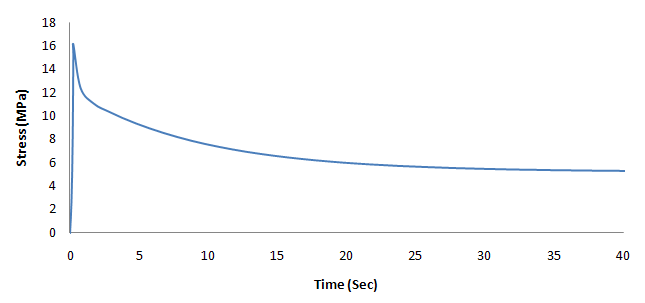
An important viscoelastic characteristic of ligaments is stress relaxation (a decline in stress over time under a constant deformation), and so a relaxation test is simulated. A uniaxial deformation is applied up to a stretch ratio of 1.12 for a very small time period (0.24 seconds) and is then allowed to relax for 50 seconds. The following figure demonstrates viscoelasticity in stress relaxation for the ACL model:

Figure 32.6: Stress Relaxation

The ACL can be injured or torn in a number of different ways. Some of the common ways are flexion and internal rotation of femur on tibia. As a soft tissue, the ACL cannot resist compressive loads. An assumption of isotropy is therefore invalid for the ACL model when analyzing knee flexion.[4]

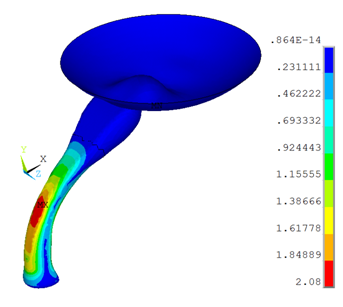
The following figure shows the stress variation in the ACL under knee flexion:

Figure 32.7: Von Mises Stresses Under 45° Knee Flexion

The femur surface rotates about the z axis, and the tibia side (the bottom part of the ACL) remains fixed. During knee flexion, an increase in von Mises stress occurs near the minimum cross sectional area of the ACL.

The femoral and tibial insertion zones are not considered, as this model emphasizes only the ACL behavior irrespective of the insertion zones. If one also considers the insertion zones, more accurate stresses near the femoral insertion zone can be expected.

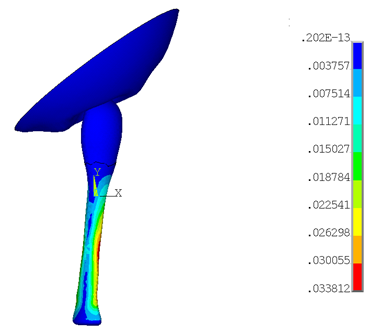
The knee joint enables leg rotation along its longitudinal axis. The cruciate ligaments limit the internal rotation.[2] The following figure shows the stress variation in the ACL under the knee rotation:

Figure 32.8: Von Mises Stresses Under 11.25° Knee Rotation

The femur surface rotates about the vertical y axis, and the tibia side remains fixed. The stress in the ligament is increased with the internal rotation of the femur.