These example problems highlight the benefits of nonlinear mesh adaptivity:
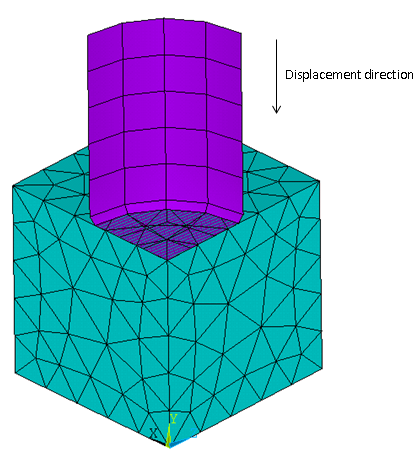
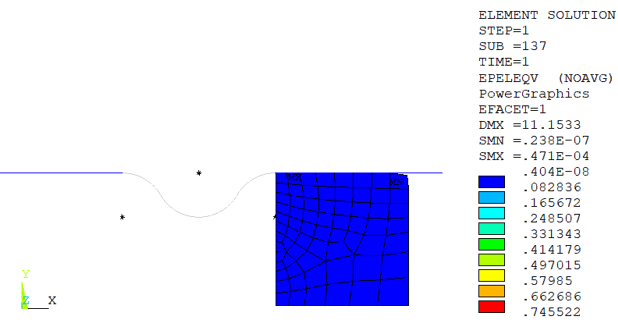
Consider a rubber seal simulation, with an initial geometry and mesh as shown:
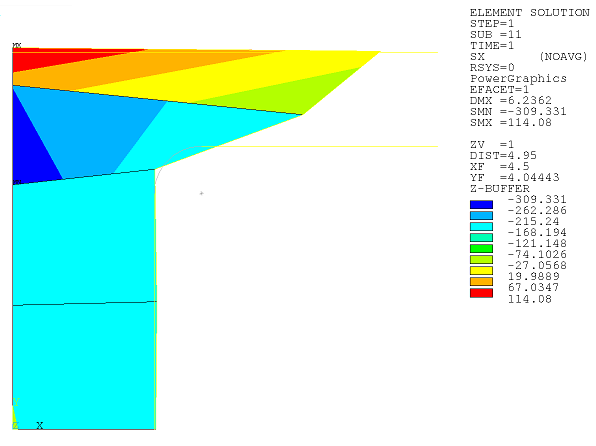
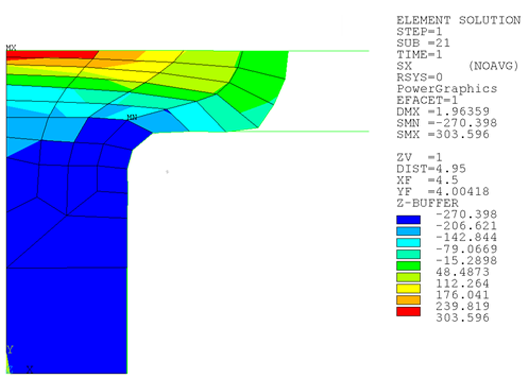
Downward displacement is applied to the rigid surface on the top of the seal. Following is the program output for the deformed seal:
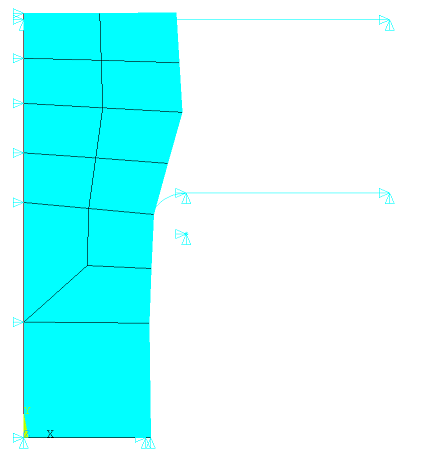
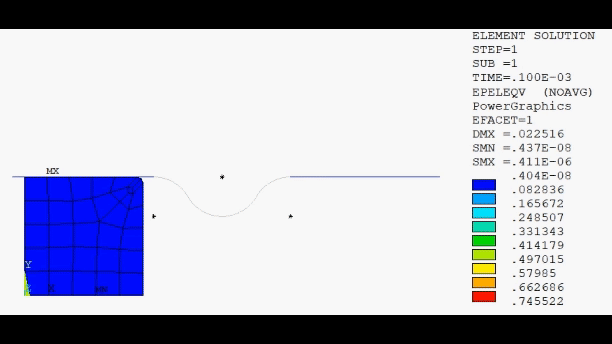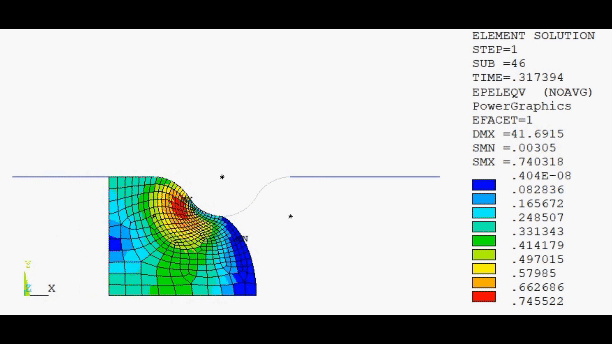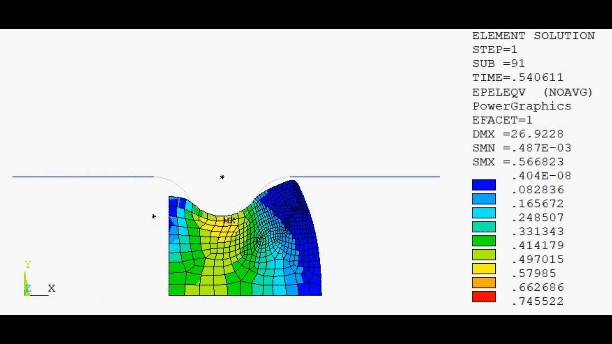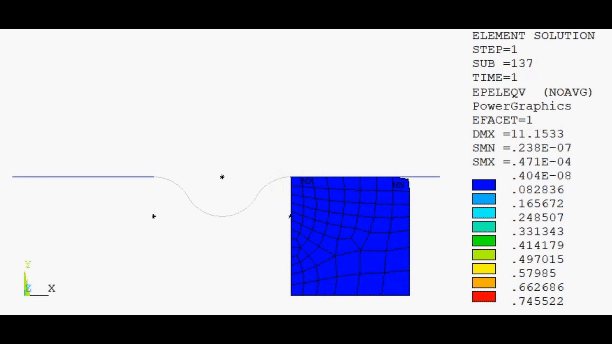
The shape of the deformed material in the gap is not realistic because the mesh is too coarse. To create a more accurate simulation, nonlinear adaptivity with position-based criteria is used to refine the mesh of the elements which will fill the gap. Two mesh refinements are performed automatically during the solution to create a more detailed mesh in the model. Following is the first mesh refinement:
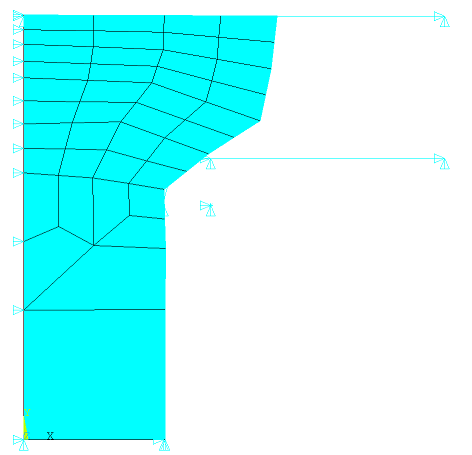
Following is the second refinement of the part of the rubber seal model that will fill the gap:
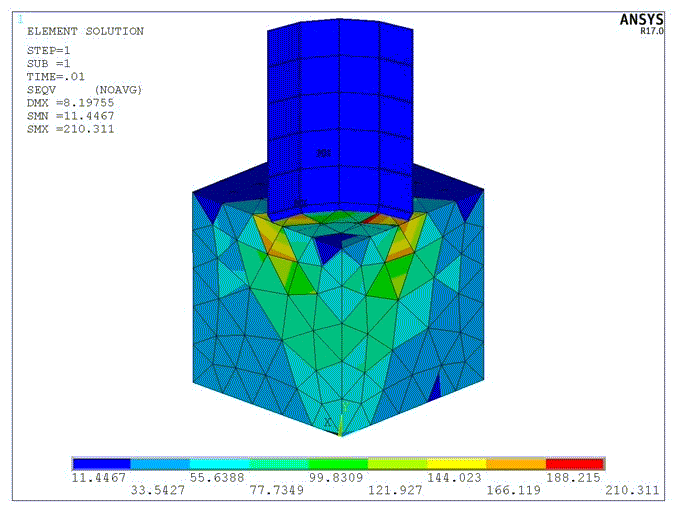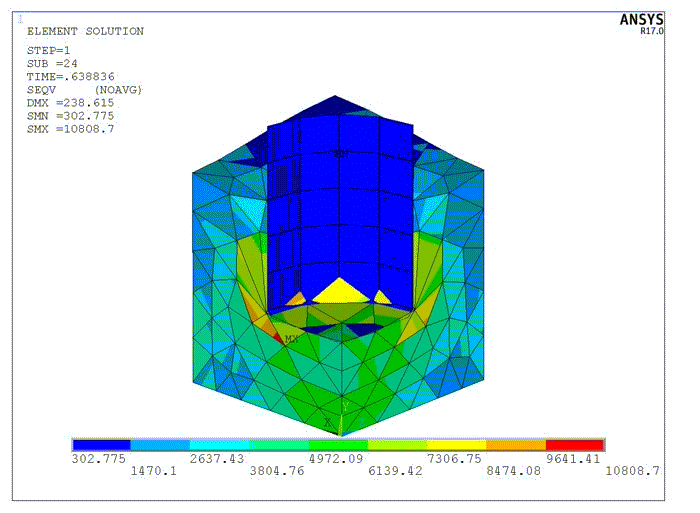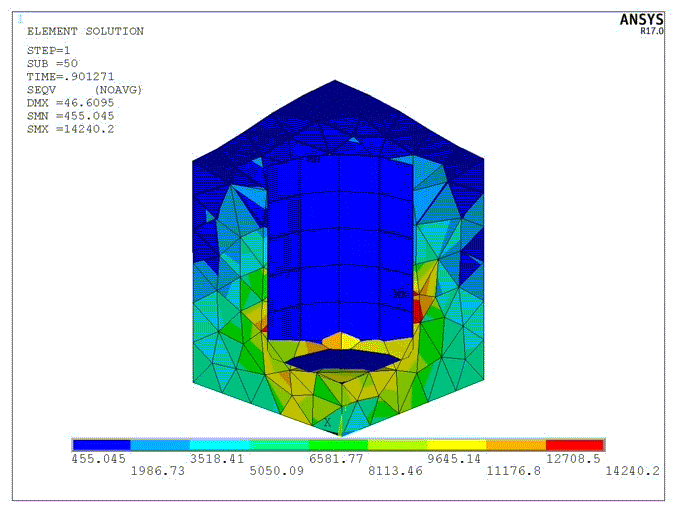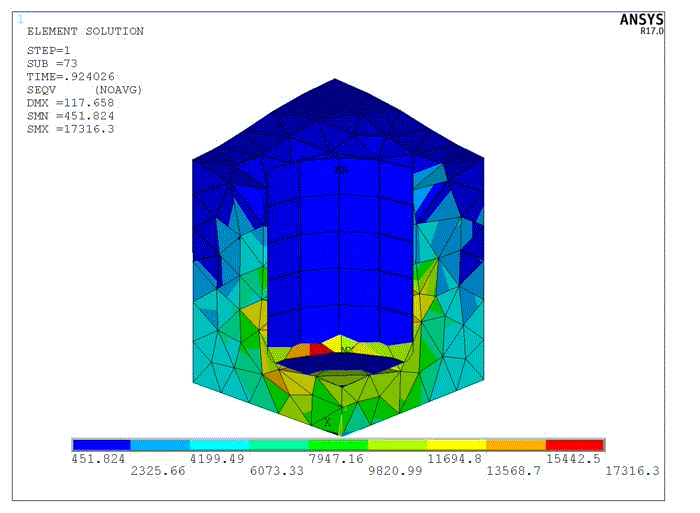
When the full load is applied in the simulation, the program outputs the following deformed seal:
With nonlinear adaptivity, the accuracy of the simulation of this type of rubber seal problem is greatly increased.
Example Input: Rubber Seal Simulation
/batch,list /prep7 /com geometry parameters rf = 1 yd = 6 yf = 12 xc = 0 yc = 12 disp = -4.0 w = 3 /com element types and size el = w et,1,182 keyopt,1,3,2 !keyopt,1,6,1 et,2,169 et,3,172 keyopt,3,9,0 keyopt,3,10,1 !keyopt,3,2,3 /com materials c10=62.3584129 c01=-37.8485452 dd=1.E-03 tb,hyper,1,,2,mooney tbdata,1,c10,c01,dd mp,mu,2,0.0 r,2 /com create the model k,1,xc,yc k,2,xc+3*w,yc k,3,w,0.0 k,4,w,yd k,5,3*w,yd rect,0,w,0,yd rect,0,w,yd,yf /pnum,line,1 l,1,2 l,3,4 l,4,5 lfillt,10,11,rf /com create mesh esize,el mat,1 type,1 real,1 amesh,1,2 /pnum,elem,1 /pnum,node,1 nummrg,node numcmp,node /replot /com the 1st contact pairs mat,2 real,2 type,2 esize,yf lmesh,9 allsel,all type,3 lsel,,,,6,7 nsll,,1 esln,,0 esurf alls /com the 2nd contact pairs real,3 type,2 lplot esize,yf lmesh,9,12 lsel,s,line, ,10,12 esll,s,1 esurf, ,reverse allsel,all lplot type,3 lsel,,,,6 lsel,a,,,2 nsll,,1 esln,,0 esurf alls /com boundary condition /com rigid punch lsel,,,,9 nsll,,1 d,all,uy,disp d,all,ux,0.0 alls /com rigid die face lsel,,,,10,12 nsll,,1 d,all,uy,0.0 d,all,ux,0.0 alls /com left side nsel,,loc,x,0 d,all,ux,0.0 alls /com bottom nsel,,loc,y,0 d,all,uy,0.0 alls /com check the contact definition cncheck elist finish /solution /com define nonlinear adaptive criterion esel,,ename,,182 cm,solid,elem allsel nlad,solid,add,box,xyzr,-0.0,9,5,12 nlad,solid,on,,,-2 pred,off rescontrol,,all,1,20 eresx,no nlgeom,on time,1 NSUBST,50,500,5 outres,all,all solv finish
Another example of the increased accuracy achieved with nonlinear mesh adaptivity involves mesh refinements in regions with high stress concentrations. For example, consider this material cracking model:
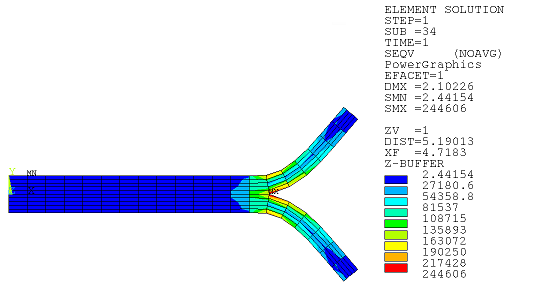
Following is the program output for the crack simulation:
The solution and solution time are:
| σx | σy | τxy | σ_VM | Elapsed Time |
|---|---|---|---|---|
| 214113 | 91103.2 | 91641.2 | 244606 | 12.00 |
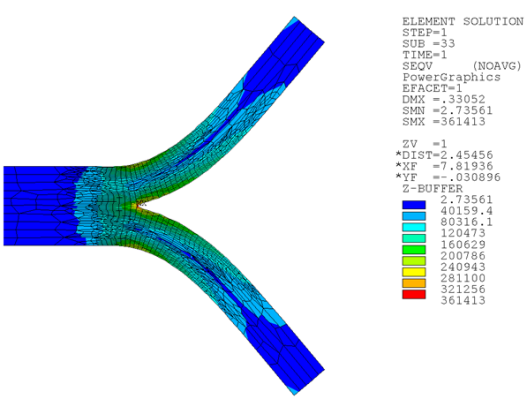
For a more accurate solution at the crack tip, nonlinear adaptivity is applied using energy-based criteria. Following is the output when three refinements are applied during solution:
The solution and solution time are:
| σx | σy | τxy | σ_VM | Elapsed Time |
|---|---|---|---|---|
| 262713 | 291816 | 164471 | 361413 | 64 |
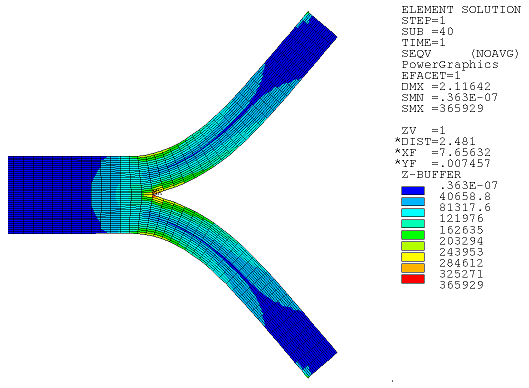
Following is the output if the same simulation is performed with a fine mesh and no nonlinear mesh adaptivity:
The solution and solution time are:
| σx | σy | τxy | σ_VM | Elapsed Time |
|---|---|---|---|---|
| 293992 | 274278 | 160033 | 365929 | 190 |
As demonstrated, nonlinear adaptivity provides sufficient accuracy, yet with drastically reduced simulation time.
Example Input: Crack Simulation
/batch,list /prep7 ! MATERIAL PROPERTIES et,1,183 keyopt,1,1,0 keyopt,1,6,1 MP,PRXY,1,0.3 MPTEMP,1,0,500 ! Define temperatures for Young's modulus MP,EX,1,12E6,-8E3 ! C0 and C1 terms for Young's modulus TB,BKIN,1,2 ! Activate a data table TBTEMP,0.0 ! Temperature = 0.0 TBDATA,1,44E3,1.2E6 ! Yield = 44,000; Tangent modulus = 1.2E6 TBTEMP,500 ! Temperature = 500 TBDATA,1,29.33E3,0.8E6 ! Yield = 29,330; Tangent modulus = 0.8E6 TBLIST,BKIN,1 ! List the data table /XRANGE,0,0.01 ! X-axis of TBPLOT to extend from varepsilon=0 to 0.01 TBPLOT,BKIN,1 ! Display the data table ! GEOMETRY blc4,0,0,10,0.5 blc4,0,0,10,-0.5 lsel,s,loc,y,0 lsel,a,loc,y,0.5 lsel,a,loc,y,-0.5 lesize,all,,,20 lsel,inve lesize,all,,,5 amesh,all elist allsel,all nsel,s,loc,y,0 nsel,r,loc,x,0,7 nummrg,node allsel,all ! COMPONENT esel,all cm,cm1,elem allsel,all esel,all cm,cm2,elem allsel,all ! LOADS nsel,s,loc,x,0 d,all,all allsel,all nsel,s,loc,y,0.5 nsel,r,loc,x,10 f,all,fy,5500 allsel,all nsel,s,loc,y,-0.5 nsel,r,loc,x,10 f,all,fy,-5500 allsel,all nplot finish /solu nlgeom,on ! large displacement analysis ON outres,all,all ! all solutions are written rescontrol,define,all,all ! write every substeps in a file eresx,no ! no interpolation for the point of integration time,1 nsubst,50,100,20 /nerr,,,,1 ! prevent the GUI for closing if no convergence ! NON LINEAR ADAPTIVITY nlad,cm2,add,energy,mean,1 nlad,cm2,on,,,-3 allsel,all solve finish ! POSTPROCESSING /post1 /out set,last nsel,s,loc,y,0 nsel,r,loc,x,0,7 esln,s,0,all presol,s,eqv finish /exit
This example problem demonstrates how to apply nonlinear mesh adaptivity to remove mesh distortion and solve problems associated with high deformation. Unlike the two prior problems, general remeshing is necessary with the mesh-quality-based criterion applied in this problem.
Consider a metal forging simulation, with an initial geometry and mesh:
The flexible block has symmetry boundary conditions on three facets. A rigid die is placed on the top of the block with applied displacement in the Y direction. It is intended to compress the block to 80 percent. Without nonlinear adaptivity, the simulation cannot converge because of high mesh distortion, as shown:
The solution diverges at approximately 40 percent load with the following error:

Nonlinear adaptivity with a mesh-quality-based criterion corrects the mesh shape caused by high distortion. To check the mesh quality at every substep, skewness is set to 0.9 (NLADAPTIVE,,,MESH,SKEWNESS,0.9). With several remeshings, the full load is successfully applied, as shown with deformation in this animation:
Example Input: 3D Metal Forging Simulation
/batch,list /PREP7 !-----------geometry parameters--------------- !mm cylinder_radius = 500 cylinder_offset = 1000 block_height = 1000 radius_fillet = 33 !---------initial meshing parameters---------- block_esize = 200 cylinder_esize = 200 !------------loading parameters--------------- cylinder_disp = -800 !------------NLAD parameters------------------ skw_ = 0.95 !skewness threshold freq = 1 !NLAD frequency (1 means check every substep) start_time = 0 !beginning time for NLAD interval end_time = 1 !end time for NLAD interval !------------remeshing parameters------------- sculpt_layers = 4 !no. of sculpting layers !************material properties************** EX=70e3 ET=7e3 EP=EX*ET/(EX-ET) MP,EX,1,EX !aluminium material properties MP,NUXY,1,0.33 !poisson's ratio MP,MU,1,0 !coefficient of friction TB,PLAS,1,,,BISO !bilinear isotropic material TBDATA,1,20 !yield stress in MPa TBDATA,2,EP !tangent modulus in MPa !------------geometry creation---------------- blc4,0,0,block_height,block_height,block_height k,9,0,cylinder_offset,0 k,10,0,cylinder_offset,cylinder_radius k,11,0,cylinder_offset+cylinder_offset,cylinder_radius k,12,0,cylinder_offset+cylinder_offset,0 l,9,10 l,10,11 l,11,12 l,12,9 lfil,13,14,radius_fillet al,13,17,14,15,16 vrotat,7,,,,,,9,12,90 !---------element types & settings------------ et,1,285 et,2,170 et,3,174 !-------------general meshing----------------- type,1 mat,1 real,1 esize,block_esize vmesh,1 !-------------contact pair 1------------------ real,2 !---------------target elements--------------- type,2 mat,2 asel,s,area,,8,10 aesize,all,cylinder_esize amesh,all alls !---------------contact elements-------------- type,3 mat,1 asel,s,area,,4 nsla,s,1 esln esurf alls !--------------create components-------------- esel,s,ename,,285 cm,comp1,elem !create NLAD component alls !-----boundary conditions & loading----------- asel,s,area,,5,6 nsla,s,1 d,all,ux,0.0 alls asel,s,area,,1,2 nsla,s,1 d,all,uz,0.0 alls asel,s,area,,3 nsla,s,1 d,all,uy,0.0 alls asel,s,area,,7,12 nsla,s,1 d,all,uz,0.0 d,all,ux,0.0 d,all,uy,cylinder_disp alls fini /SOLU !-----------general solution settings--------- nlgeom,on eresx,no outres,all,all !---------------NLAD settings----------------- !check NLAD parameters section above for values nlad,comp1,add,mesh,skew,skw_ !nlad with mesh-quality-based criterion nlad,comp1,on,,,freq,start_time,end_time !------------remeshing settings--------------- !check remeshing parameters section above for values nlmesh,nlay,sculpt_layers !---------------step settings----------------- time,1 nsubst,100,10000,10 alls solve fini !---------------POSTPROCESSING---------------- /POST1 set,list fini /exit
This example problem demonstrates the benefits of nonlinear mesh adaptivity for simulating cases with very high deformation. The 2D problem uses a generalized plane strain extrusion model.
The flexible block of height = 19.5 will be compressed on the right side by a rigid die (where applied displacements = 30) to reduce its height to 6.5:
The bottom of the block has a symmetric boundary condition, the die is a frictionless rigid, and the material is elastoplastic.
Without nonlinear adaptivity, the solution diverges at approximately 80 percent load due to mesh distortion, generating the following error message:

Nonlinear adaptivity with a mesh-quality-based criterion corrects a highly deformed mesh shape. To check the mesh quality at every substep, the maximum corner angle of the mesh shape is set to 155 (NLADAPTIVE,,,MESH,SHAPE,155). With several remeshings (depending on the platform), the full load is successfully applied:
Example Input: 2D Metal Extrusion Simulation
/batch,list /PREP7 h1=19.5 b1=45 h2=6.5 b2=22.5 b3=5 h3=17 el=h1/8 et,1,182 keyopt,1,3,5 keyopt,1,6,1 EX=1.0e+6 ET=1.0e4 EP=EX*ET/(EX-ET) mp,ex,1,1.0e+6 mp,nuxy,1,0.3 tb,plas,1,,,biso TBDATA,1,8.0e2,EP /com --- Rigid target k,1,0,h1 k,2,b1,h1 k,3,b1+b2,h2 k,4,b1+b2+b3,h2 k,5,b1+b2+b3,h3 l,1,2 l,2,3 l,3,4 l,4,5 LFILLT,1,2,5, , LFILLT,2,3,5, , /pnum,line,1 /com --- Rectangular block k,10,0,0 k,11,b1,0 k,12,b1,h1 k,13,0,h1 l,10,11 l,11,12 l,12,13 l,13,10 lfillt,8,9,el al,7,8,11,9,10 esize,el real, 1 mat, 1 type, 1 amesh, 1 /com --- Element type definitions for contact pair et,2,169 et,3,172 /com --- Mesh target surface mat, 2 real, 2 type, 2 lmesh,1,6 /com --- Create contact elements type,3 real, 2 lsel, s, line, , 8,9 lsel, a, line, , 11 nsll,,1 esln,,0 esurf alls /com --- Apply Constraints nsel,s,loc,y d,all,uy,0.0 alls lsel,s,line,,1,6 nsll,,1 d,all,all,0.0 alls nsel,s,loc,x d,all,ux,30 alls esel,s,ename,,182 cm,c1,elem !create NLAD component alls fini /SOLU nlgeom,on eresx,no pred,off outres,all,all time,1 NSUBST,20,1000,5 alls gsgdata,2,0,0,0,0 gsbdata,lfiber,0,rotx,0,roty,0 gslist,geometry gslist,bc alls !-----Nonlinear Adaptive Region cmsel,all nlad,c1,add,mesh,shape,160,10,70 !nlad with mesh-quality-based criterion nlad,c1,on,,,1,0,1 nlmesh,nlay,100 !no. of sculpting layers nlmesh,grad,0 !option for mesh gradient control nlmesh,srat,0.9 !control global sizing of new mesh nlad,all,list,all nlmesh,list alls SOLVE fini /POST1 set,list fini /exit
This example problem using nonlinear mesh adaptivity simulates high mesh-deformation with coupled structural-thermal degrees of freedom. The analysis uses the 2D coupled-field element PLANE222 with structural-thermal coupling and plane strain options.
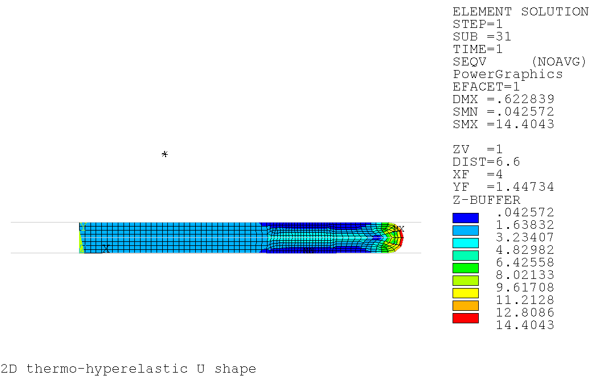
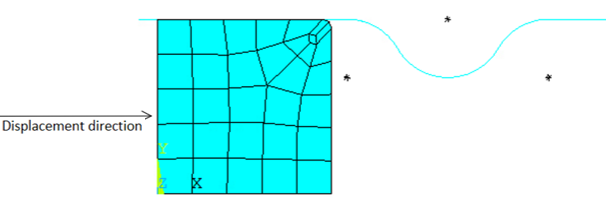
A U-shape workpiece is compressed between two rigid and frictionless target surfaces. The top target surface is displaced in the negative y direction to compress the workpiece to reach a state of complete self-contact. A temperature difference is applied on the top and bottom surfaces. Temperature-dependent thermal material properties are defined in the model.
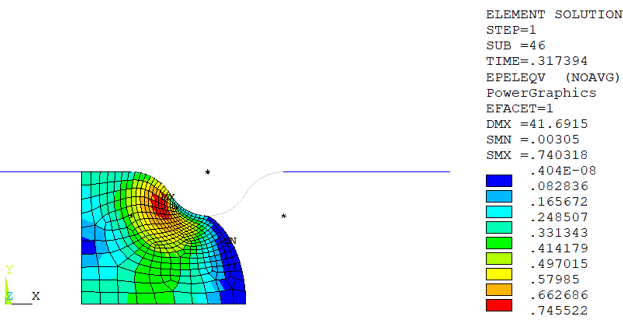
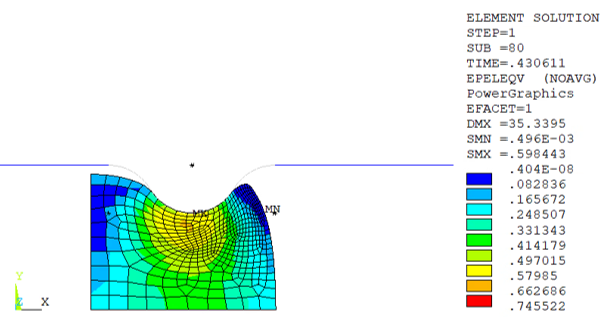
Without nonlinear adaptivity, the highly deformed mesh shape leads to a diverged solution. A mesh-quality-based criterion defined by nonlinear adaptivity measures the mesh quality and verifies a maximum corner angle of 150 degrees (NLADAPTIVE,ADD,,MESH,SHAPE,150) at every substep. With refined meshing, the solution can converge with the total displacement load applied.
Example Input: Compression of 2D Thermo-Hyperelastic U-Shape Simulation
/batch,list /title, 2D thermo-hyperelastic U shape /prep7 /nopr h=0.5 b = 4 x0 = 0.0 y0 = 0.0 x1 = 5.0 y1 = x0+h y2 = x0+h+b et,1,222,11 keyo,1,3,2 keyo,1,11,1 tb,hype,1,1,3,ogde tbdata,1,3.2084e-009,7.281,0.035198,3.0149,6.3712,2.0493 mptemp,1,100,200,300,400,500 mpdata,alpx,1,1,2.568e-6,3.212e-6,3.594e-6,3.831e-6,3.987e-6 mpdata,kxx,1,1,14.64,9.83,7.32,5.75,4.92 ! upper contact pair et,2,169 r,2 et,3,172 keyo,3,1,1 ! ux/uy/temp keyo,3,9,0 keyo,3,10,0 mp,mu,2,0.0 ! lower contact pair et,4,169 r,3 et,5,172 keyo,5,1,1 ! ux/uy/temp keyopt,5,9,0 keyopt,5,10,0 mp,mu,3,0.0 ! self-contact pair et,6,169 r,4 rmodif,4,14,10.0 et,7,172 keyo,7,1,1 ! ux/uy/temp keyopt,7,9,0 keyopt,7,10,0 mp,mu,4,0.0 et,8,169 r,5 rmodif,5,14,10.0 et,9,172 keyo,9,1,1 ! ux/uy/temp keyopt,9,9,0 keyopt,9,10,0 mp,mu,5,0.0 ! Geometry ! keypoints k, 1, x0, y0 k, 2, x1, y0 k, 3, x0, y0+h k, 4, x1, y0+h k, 5, x0, y2 k, 6, x1, y2 k, 7, x0, y2+h k, 8, x1, y2+h k, 9, x1, y0+h+b/2 k, 10, x1, y0+h+b/2, y0+h+b/2 circle, 9, , 10, 4, 180 circle, 9, , 10, 2, 180 ! line definitions l, 1, 14 l, 3, 11 l,1, 3 l, 13, 5 l, 16, 7 l, 5, 7 l,11,14 l,13,16 l,12,15 ! area definitions al,5,11,6,7 al,3,13,1,11 al,4,12,2,13 al,8,12,9,10 esize,0.15 real,1 mat,1 type,1 amesh,all asel,s,area,,2,3 esla,s esel,r,type,,1 cm,cm222,elem alls ! contact definitions k, 17, x0-2.0, y0 k, 18, x1+5.0, y0 k, 19, x0-2.0, y0+h+h+b k, 20, x1+5.0, y0+h+h+b l, 18, 17 l, 19, 20 ! 1st contact pair -- top surface pair mat,2 real,2 type,2 ! mesh target surface lmesh,15 ! define pilot node *get,PilotKpt,kp,,num,max PilotKpt=PilotKpt+1 k,PilotKpt,x0+x1/2,y0+h+h+b+2.0 *get,PilotID,node,,num,max PilotID=PilotID+1 nkpt,PilotID,PilotKpt tshap,pilo e,PilotID ! define contact elements type,3 real,2 lsel,s,line,,4 lsel,a,line,,9 nsll,,1 esln,,0 esurf alls ! second contact pair --- bottom pair mat,3 type,4 real,3 ! mesh target surface lmesh,14 ! mesh contact elements type,5 real,3 lsel,s,line,,5 lsel,a,line,,3 nsll,,1 esln,,0 esurf alls ! 1st self-contact pair mat,4 type,6 real,4 lsel,s,line,,6,8,2 nsll,,1 esln,,0 esurf alls type,7 real,4 lsel,s,line,,6,8,2 nsll,,1 esln,,0 esurf alls ! 2nd self-contact pair mat,5 type,8 real,5 lsel,s,line,,1,2 nsll,,1 esln,,0 esurf alls type,9 real,5 lsel,s,line,,1,2 nsll,,1 esln,,0 esurf alls ! Initial boundary conditions d,PilotID,ux,0.0 d,PilotID,uy,-4.1 d,PilotID,rotz,0.0 nsel,s,loc,x,0. d,all,ux,0. alls tref,20.0 DL,14,,temp,100 DL,15,,temp,500 alls cnch,auto rmodif,4,14,1000.0 rmodif,5,14,1000.0 fini /solu /nopr nlad,cm222,add,mesh,shape,150 nlad,cm222,on,,,1 nlmesh,nlay,10 nlmesh,srat,0.8 nlmesh,bdra,10 nlmesh,grad,2 nlgeom,on eresx,no time,1 nsub,20,100,5 rescontrol,define,all,all outres,all,all solve fini /post1 set,list finish /exit,nosave
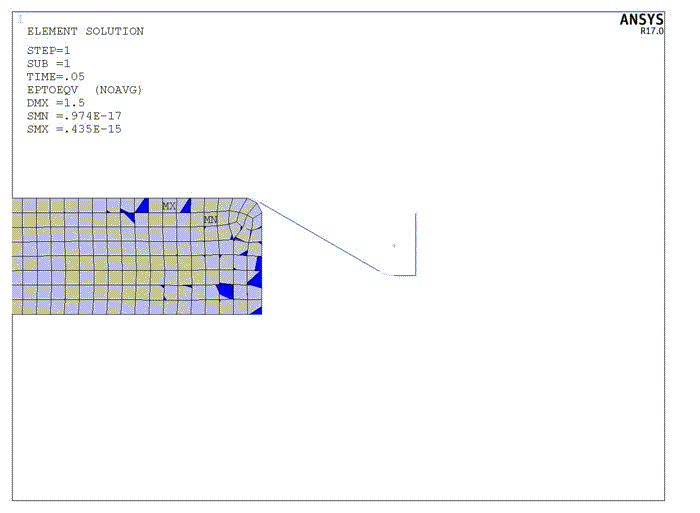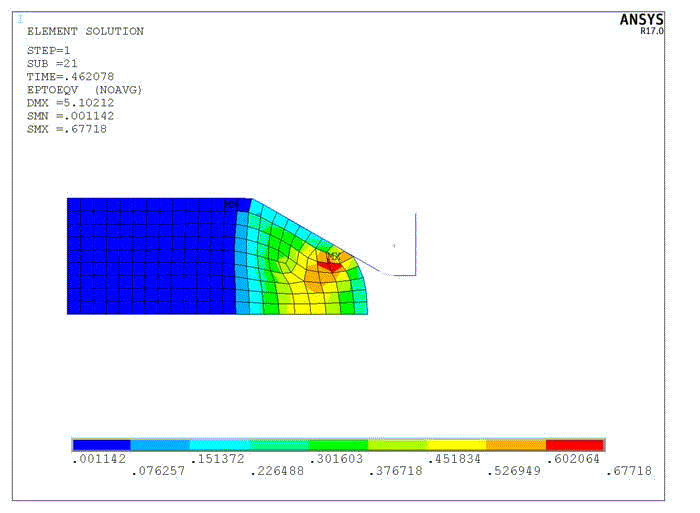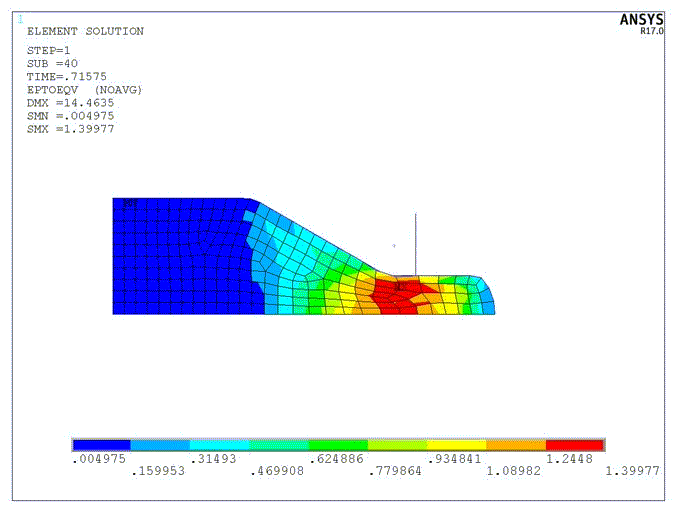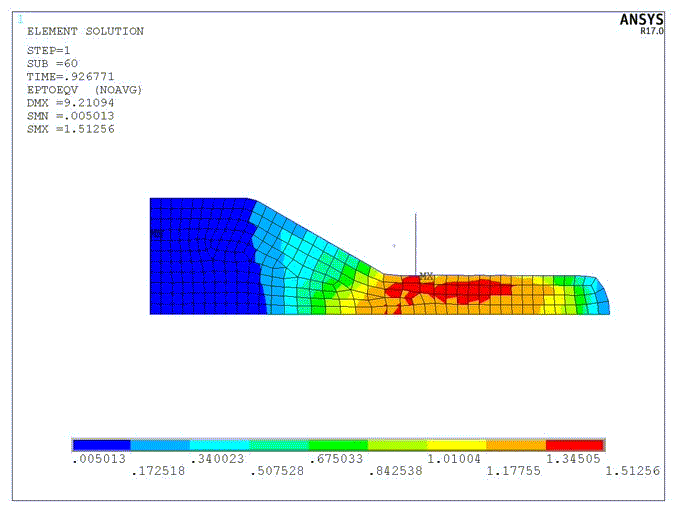
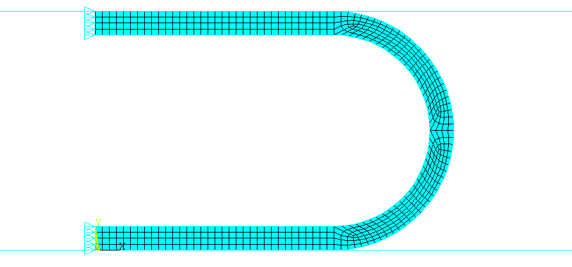
This example demonstrates the benefits of nonlinear adaptivity with mesh coarsening in addition to mesh refinement and mesh-quality improvement. The 2D problem uses a hyperelastic material (rubber) which is pushed from the left through a narrow channel. The bottom of the block has a symmetric boundary condition. The contact to the channel has friction.
During the analysis, the mesh is adapted to improve the quality of deformed elements and the solution quality in regions of interest (high strain energy). Without nonlinear adaptivity, the solution diverges due to mesh distortion, when the rubber is deformed upon entering the narrow channel (at approximately 30 percent of applied load).
At the end of the analysis, the mesh is adapted to reduce the numerical effort (coarsening the mesh) for elements that have passed the narrow channel and where a refined mesh is no longer required to obtain a high-quality solution.
Example Input: 2D Rubber Extrusion Simulation
/batch,list /prep7 /com, --- Geometry parameters ly=100 lx=ly g0=0.1*lx l2=1.5*lx gy=0 rad=ly/3 rad0=rad !fillet radius of the rigid target rad1=5 !fillet radius of the solid g1=rad0 !g1 has to be min rad0 due to fillet /com, --- Meshing parameters es=20 !general element size div=2 !nb divisions per solid fillet /com, --- Material parameter tb,hyper,1,,2,ogden !td2 values tbdata,1,2.8 tbdata,2,7.9 tbdata,3,-1.86e2 tbdata,4,-1.85 tbdata,5,1.e-5 ! incompressibility parameter mp,mu,2,0.1 ! fric coeff for contact elements /com, --- Element definition et,1,182 keyopt,1,1,0 ! full integration Bbar method keyopt,1,3,2 ! plane strain keyopt,1,6,1 ! mixed u-p formulation et,2,172 keyopt,2,10,2 ! cont. stiffness update: each iteration keyopt,2,15,3 ! cont. stabilization: damping active et,3,169 /com, --- Contact real constants pinb=1.0 !scale factor for the default pinball size r,11,,,,,,pinb r,12,,,,,,pinb /com, --- Geometry k,1,0,0 k,2,lx,0 k,3,lx,ly k,4,0,ly k,5,-g0,ly+gy k,6,lx+g1,ly+gy k,7,lx+g1+rad,ly-rad+gy k,8,lx+g1+2*rad,ly+gy k,9,lx+g1+2*rad+l2,ly+gy k,11,lx+g1+rad,ly+gy k,10,0,0 k,12,0,ly+gy l,1,2 l,2,3 l,3,4 l,4,1 l,5,6 larc,6,7,11,rad larc,7,8,11,rad l,8,9 lfillt,5,6,rad0 lfillt,7,8,rad0 l,10,12 lfillt,2,3,rad1 ! solid fillet al,1,2,12,3,4 ! single fillet /com, --- Meshing type,1 esize,es mshape,0,2-D ! 0-Quadrilaters lsel,s,line,,12 ! single solid fillet lesize,all,,,div amesh,all mat,2 real,11 type,2 lsel,s,line,,2,4,1 lsel,a,line,,12 nsll,s,1 esurf allsel type,3 lmesh,5,10,1 ldele,11 /com, --- Boundary conditions esel,s,type,,1 nsle,s,all nsel,r,loc,y d,all,uy esel,s,type,,1 nsle,s,all nsel,r,loc,x cm,my_nodes,node allsel cmsel,all finish /com, --- Solution parameters /solution antype,static nlgeom,on outres,all,all rescontrol,define,all,1 eresx,no nropt,unsym,,off time,1 pred,off nsubst,10000,100000,100 cmsel,s,my_nodes d,all,ux,225 allsel cmsel,all /com, -- Nonlinear Adaptivity settings esel,s,type,,1 ! all solid elements cm,cm2enrg,elem ! Refinement cm,cm2coar,elem ! Distortion cm,cm2mesh,elem ! Coarsening allsel cmsel,all nlad,cm2enrg,add,energy,mean,1.e-10 nlad,cm2enrg,on,,,-2,0,0.3 nlad,cm2mesh,add,mesh,shape,150 nlad,cm2mesh,on,,,1 nlad,cm2coar,add,box,xyzr,225,300,0,100,,,coar nlad,cm2coar,on,,,-5,0.7,1. nlmesh,nlay,7,3 nlmesh,srat,,,2. allsel cmsel,all /com, --- Solution process solve finish