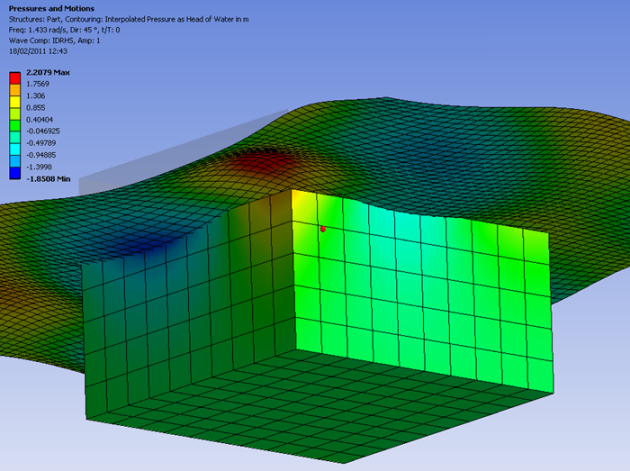
In this example, a 30m x 30m x 22.5m box with 7.5m above the water level (z = 0m) was modeled in a hydrodynamic diffraction analysis.
The following conditions exist:
The diffracting elements are 3m x 3m.
Waves are defined in eight directions and four frequencies (0.031, 0.5, 0.97, and 1.43 rad/s).
Forward speed and hydrostatic pressures are not included.
The pressure results from the hydrodynamic diffraction analysis are 45°, 1.43 rad / s, t / T = 0, as shown in the following figure:
The diffracted wave loading data in the analysis_1.ahd file is imported (OCREAD) and applied to the structural model for further analysis, as shown in the following example input:
/verify,difwaveeg /FILNAME,difwaveg /prep7 /TITLE,difwaveeg, EXAMPLE FOR AQWA LOADING /com ************************************************************************** /com SHELL MODEL OF A HOLLOW BOX TUBE /com CREATED 20/05/10 /com ************************************************************************** antype,static nlgeom,off ! define shell section sectype,11,shell secdata,0.1 ! define ocean matwat=2 idwat=2 idcur=3 idwav=4 depth=250.0 ! define geometry /prep7 !wpoff,,,-15 k,,-15,-15,-15 k,,15,-15,-15 k,,15,15,-15 k,,-15,15,-15 l,1,2 l,2,3 l,3,4 l,4,1 k,,-15,-15,0 l,1,5 k,,-15,-15,7.5 l,5,6 adrag,1,2,3,4,,,5,6 a,1,2,3,4 ! Mesh et,1,181 type,1 mat,1 secnum,11 esize,1 amesh,all et,2,154 keyopt,2,4,1 keyopt,2,8,idwat r,2 rmore,0.0001 type,2 mat,1 real,2 esurf ! steel material properties MP,EX, 1,2.1e11 MP,PRXY,1,0.3 MP,ALPX,1,0.0 MP,DENS,1,7800.0 ! water density mp,dens,matwat,1025.0 ! supports d, 1,ux d, 2,ux d,977,ux d,497,ux d, 1,uy d, 2,uy d,977,uy d,497,uy d, 1,uz d, 2,uz d,977,uz d,497,uz finish ! /SOLU ! CASE 4 H=1 T=4.384199 PH=0 D=45 acel,0,0,9.8 ! ocean octype,basic,ocean1 ocdata,depth,matwat !! diffracted wave octype,wave ocdata,8,45.0 octable,1.0,200,0.0 ! !! ocread to read in external data file ocread,analysis_1,ahd ! ! list all slist,all oclist,all !! apply inertia relief !! irlf,1 NSUBST,1,1 ! 1 SUBSTEPS TIME,1.0 OUTPR,all,1 OUTRES,all,1 solve finish /post1 etable,x,smisc,13 pletab,x,avg
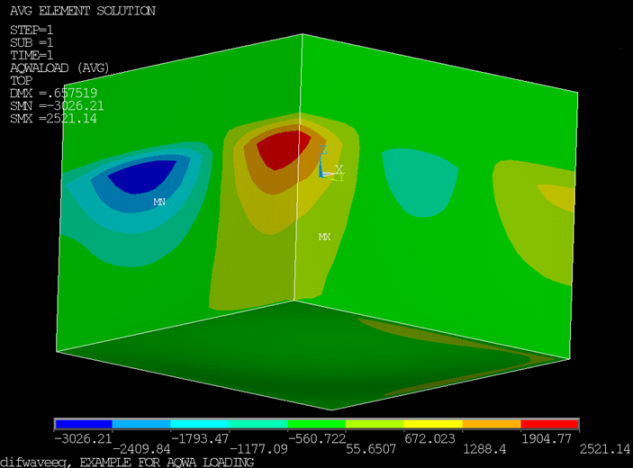
The following figure shows the analysis results using the pressures from the diffracted wave: