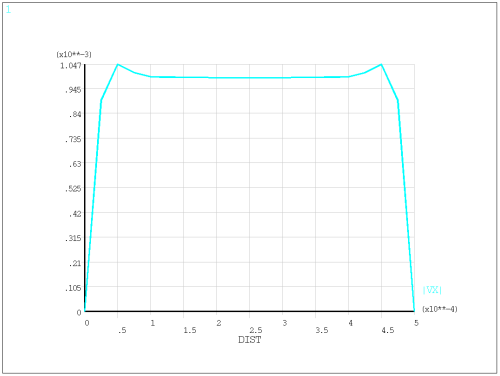
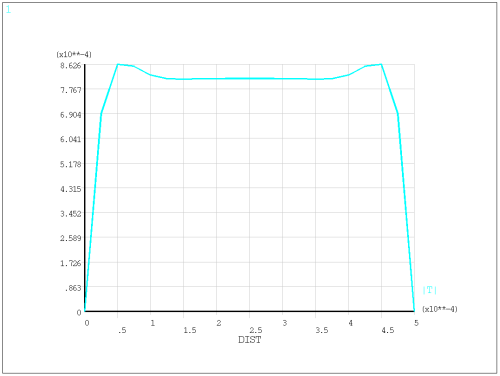
This example uses the FLUID220 element to demonstrate the sound characteristics in a thin gap solved by the FLNS model.
A thin 2D gap has one closed end with zero normal velocity, and a unit pressure is applied to the other end. The height of the gap is 0.5 mm, and the length is 2 mm.
The air material properties are as follows:
| Mass density = 1.2256 kg/m3 |
| Speed of sound = 340.6 m/s |
| Dynamic viscosity = 17.83×10-6 Pa·s |
| Thermal conductivity = 0.02534 W/(m·K) |
| Specific heat at constant pressure = 1005 J/(kg·K) |
| Specific heat at constant volume = 718 J/(kg·K) |
| Bulk viscosity = 10.698×10-6 Pa·s |
The quiescent temperature is 15 °C, and the quiescent pressure is 101,325 Pa.
The 3D FLNS model is solved at 10 kHz and is verified with the low reduced frequency (LRF) model [1].
/batch,list /nopr /prep7 ! Define the viscous-thermal material c0 = 340.6 rho = 1.2256 visc = 17.83e-6 kxx = 0.02534 cp = 1005 cv = 718 bvis = 0.6*visc tb,afdm,1,,,mat tbdata,1,rho,c0,visc,kxx,cp,cv tbdata,7,bvis ! ! Create the model and mesh it h0 = 0.25e-3 L = 2.e-3 h=h0/10 et,1,220,,6 ! Define viscous-thermal element type block,0,L/2,0,h,-h0,h0 block,L/2,L,0,h,-h0,h0 vglue,all esize,h vmesh,all allsel ! nsel,s,loc,x,L-1.e-3*h,L+1.e-3*h sf,all,pres,-1 ! Apply pressure allsel nsel,all bf,all,temp,15 ! Quiescent temperature bf,all,spre,101325 ! Quiescent pressure toffst,273 nsel,s,loc,x,0 d,all,vx,0 allsel d,all,vy,0 ! Zero y component of velocity allsel ! ! Define BC on rigid wall nsel,s,loc,z,-h0 nsel,a,loc,z,h0 d,all,temp,0 d,all,vx,0 d,all,vz,0 alls finish ! ! Solve the harmonic analysis /solu eqslv,sparse antype,harm hropt,full harfrq,10000 solve finish ! ! Plot out velocity and temperature in POST1 /post1 set,1,1,,ampl path,path,2 ppath,1,,L,0,-h0 ppath,2,,L,0,h0 pdef,|vx|,v,x pdef,|T|,temp /show,png,rev plpath,|vx| plpath,|T| finish