This example uses the FLUID30 and SHELL181 elements in a transient analysis to calculate the hydrostatic pressure of a water container. The sloshing effect is simulated by applying a free surface (SF,,FREE) to the pressure-based acoustic elements and defining acceleration due to gravity.
The shell and acoustic elements model the container and water, respectively, with these dimensions:
| container height = 10 m |
| container radius = 5 m |
| wall thickness = 0.1 m |
| water depth = 8 m |
| Material Properties | |
| Container | Water |
| Elastic modulus = 210 GPa | Mass density = 1000 kg/m3 |
| Major Poisson's ratios = 0.3 | Speed of sound = 1500 m/s |
| Mass density = 7800 kg/m3 | |
The bottom of the container is fixed. The interfaces between the structure and the water are flagged with the fluid-structure interaction surface load (SF,,FSI).
To obtain a stable hydrostatic pressure status in a transient analysis:
The ramped gravitational acceleration must be applied during the first period, then kept constant for the rest of solution time.
The time increment must be unchanged during the entire solution.
If a transient sloshing problem is solved, other loads should be applied after the stable hydrostatic pressure status is reached.
/batch /nopr /prep7 z_bottom=-8 !position of the bottom p_radius=5 !radius of the container p_height=10 !Height of the container p_depth=8 !depth of water p_thick=0.01 !thickness of the container p_nh1=8 !number of mesh in vertical direction below water surface p_nh2=2 !number of mesh in vertical direction above water surface p_nr=6 !number of mesh in radial and circumferential direction z_ws=z_bottom+p_depth z_top=z_bottom+p_height ! container material property mp,ex,1,2e11 mp,prxy,1,0.3 mp,dens,1,7800 ! water material property mp,dens,2,1000 mp,SONC,2,1500 ! define elements et,1,shell181 et,2,fluid30,0,0 sectype,1,shell,,Sec1 secdata, p_thick,1,0.0,3 secoffset,MID ! create model wpoffs,0,0,z_bottom cyl4,0,0,,,p_radius,360,p_height wpoffs,0,0,p_depth vsbw,all vsel,s,loc,z,z_ws,z_top vdele,all asel,s,loc,z,z_top adele,all allsel,all ! create the geometry wprot,0,0,90 asbw,all vsbw,all wprot,0,90,0 asbw,all vsbw,all wpcsys,-1,, lsel,s,loc,z,z_bottom lsel,a,loc,z,z_ws lsel,a,loc,z,z_top lesize,all, , ,p_nr, , , , ,1 lsel,all lsel,u,loc,z,z_bottom lsel,u,loc,z,z_ws,z_top lesize,all, , ,p_nh1, , , , ,1 lsel,all lsel,u,loc,z,z_top lsel,u,loc,z,z_bottom,z_ws lesize,all, , ,p_nh2, , , , ,1 lsel,all ! mesh type,1 mat,1 secnum,1 mshape,0,2d mshkey,1 asel,s,ext asel,a,loc,z,z_ws,z_top asel,u,loc,z,z_ws amesh,all allsel,all type,2 mat,2 mshape,0,3d mshkey,1 vmesh,all allsel,all ! group the fsi nodes csys,1 nsel,s,loc,x,p_radius nsel,a,loc,z,z_bottom cm,n_fsi,node nsel,s,loc,z,z_ws cm,n_ws,node allsel,all ! set constrains on the bottom nsel,s,loc,z,z_bottom d,all,ux,0 d,all,uy,0 d,all,uz,0 allsel,all ! flag fsi surface eslv sf,n_fsi,fsi ! flag sloshing surface sf,n_ws,free allsel,all save finish /solu antyp,trans trnopt,full ! ramped gravity acceleration for first load step kbc,0 acel,0,0,9.8 timint,on time,5 delt,0.25 outres,all,all solve ! keep constant gravity acceleration time,7 kbc,0 acel,0,0,9.8 solve ! continue the constant gravity acceleration time,9 acel,0,0,9.8 solve finish /com,**** analytic result ***** pres=1000*9.8*p_depth *msg,info,pres Pressure %g
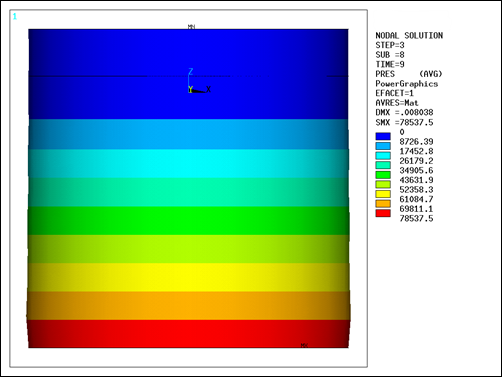
The hydrostatic pressure is given by , where ρ is the mass density of water, g is the acceleration due
to gravity, and η is the displacement from the sloshing surface. For this example,
the maximum analytic pressure is 78400 Pa. The maximum calculated pressure is 78537 Pa
at time = 9 seconds.