7.2. Absorbing Boundary Condition (ABC)

An exterior acoustics problem typically involves an infinite, homogenous, inviscid fluid. The pressure wave must satisfy the Sommerfeld radiation condition. A typical approach to such a problem involves truncating the unbounded domain by introducing a second-order absorbing element (FLUID130 or FLUID129) on the boundary Γ_a at some distance from the structure.

For a 3D acoustic analysis, the absorbing boundary must be a spherical enclosure centered at the origin (x₀,y₀,z₀) with radius r_a.

For a 2D acoustic analysis, the absorbing boundary must be a circle centered at the origin (x₀,y₀,0) with radius R_a.

Absorbing elements have a mesh conforming to the underlying elements:

The 4-node element FLUID130 (KEYOPT(1) = 0) is applied to the top of the 8-node element FLUID30.
The 8-node element FLUID130 (KEYOPT(1) = 2) is applied to the top of the 20-node element FLUID220 or the 10-node element FLUID221.
The 2-node element FLUID129 (KEYOPT(1) = 0) is connected to the 4-node element FLUID243.
The 3-node element FLUID129 (KEYOPT(1) = 2) is connected to the 8-node element FLUID244.

The absorbing elements must be on a single continuous spherical surface or circular arc.

Generate the absorbing elements as follows:

Mesh the model:
- Mesh the 3D model enclosed by a spherical surface with FLUID30, FLUID220, or FLUID221 elements.
- Mesh the 2D model enclosed by a circular arc with FLUID243, or FLUID244 elements.
Select the underlying nodes and elements on the spherical boundary surface or circular arc (lines).
Generate a surface absorbing element with the ESURF command.

Example 7.9: Generating an Absorbing Element

et,1,220,,1                   ! FLUID220
et,2,130,2                    ! second-order FLUID130
r,1,1e-6
r,2,DIM_DISTANCE              ! radius of sphere 
mp,sonc,1,1500                ! sound speed
mp,dens,1,1000                ! density
mpcopy,,1,2                   ! copy material 1 to 2
                              ! create 1/8 sphere
sphere,,DIM_DISTANCE,0,90     ! sphere
vsbw,all
vsel,s,loc,z,0,-DIM_DISTANCE
vdele,all,,,1
allsel,all
esize,DIM_ESIZE
vmesh,all                     ! mesh sphere with FLUID220
csys,2                        ! activate spherical coordinate
asel,s,loc,x,DIM_DISTANCE     ! select area on the sphere
csys,0                        ! activate Cartesian coordinate
nsla,s,1                      ! nodes attaching to area
                              ! create surface mesh
type,2                        ! FLUID130
real,2                        ! real constant 2
mat,2                         ! material 2
esurf                         ! generate surface element
allsel,all

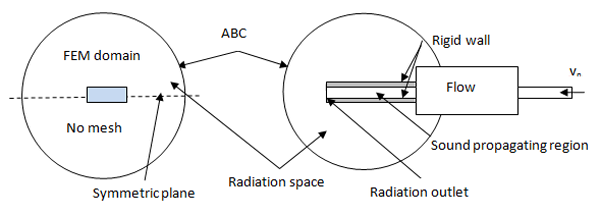
Absorbing elements accommodate the symmetry of the model. If the radiated acoustic field has no significant effect on the excitation source entity, the spherical absorbing boundary can locally enclose the open space near the radiation outlet, as shown in this figure:

Figure 7.1: Spherical ABC for Symmetry and Near the Radiation Outlet

FLUID130 and FLUID129 can be used for modal, harmonic, and transient analyses.

In a coupled harmonic analysis, the FLUID130 element is compatible with the symmetrical formulation of the FLUID30, FLUID220 and FLUID221 elements (KEYOPT(1) = 2), and the FLUID129 element is compatible with the symmetrical formulation of the FLUID243 and FLUID244 elements (KEYOPT(1) = 2). The symmetrical formulation leads to 2x performance improvement for factorization compared with the unsymmetrical solver.

For more information, see Absorbing Boundary Condition (ABC) in the Mechanical APDL Theory Reference.