As with an isotropic yield criteria that includes work hardening, we can use a uniaxial tension test to obtain the relationship between and . In practice the master curve can be calculated from any normal or shear stress-strain test. In this example we choose to use a 0° uniaxial tension test.

In this case the quadratic yield function Equation 3–29 reduces to,

(6–3)

and using the definition of effective stress Equation 3–38, the relationship between effective stress and σ₂₂ is

(6–4)

In general for uniaxial loading the following relationship results:

(6–5)

and, from Equation 3–33 the associated incremental plastic strain components are

(6–6)

On substitution of Equation 6–6 into the expression for incremental effective plastic strain Equation 3–40 we find that for uniaxial loadings

(6–7)

For pure shear loading the same arguments result in the following relationship for effective stress and effective plastic strain increment,

(6–8)

(6–9)

where rr = 44, 55, or 66 depending on shear stress components.

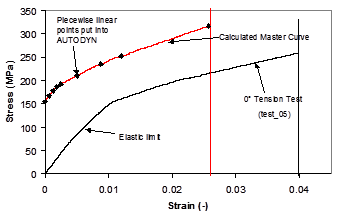
Derivation of the plasticity parameters is best illustrated by an example. In the following discussion results from tension tests on a 0°/90° woven Kevlar-epoxy composite material are presented [2]. In this case the stress-strain behavior in the 0°, or 22 direction, is considered to define the master curve. The plasticity parameter a₂₂ in this case is a free parameter and we are at liberty to set its value simply to 1.0. Equation 6–5 and Equation 6–6 are now used to transform the measured values of σ₂₂ and ε₂₂ into effective stresses and effective incremental plastic strains thus determining the required master curve, as shown in Figure 6.1: Derivation of Master Relationship from Uniaxial Tension Test.

Figure 6.1: Derivation of Master Relationship from Uniaxial Tension Test

Kevlar-epoxy is a 0°/90° woven material and is assumed to be transversely isotropic, therefore a₂₂ = a₃₃ = 1.0. The in-plane plastic Poisson’s ratio was calculated as 0.26 from 0° tension tests where strain was measured in both in-plane directions. It was calculated from the average gradient of measured strains immediately after yielding (see Figure 6.2: Longitudinal Versus Transverse Strain Measured in 0° Tension Tests. Red Line Indicates Region used to Calculate Value for In-Plane Poissons Ratio. (Picture Courtesy of EMI [2])).

Figure 6.2: Longitudinal Versus Transverse Strain Measured in 0° Tension Tests. Red Line Indicates Region used to Calculate Value for In-Plane Poissons Ratio. (Picture Courtesy of EMI [2])

Therefore from Equation 3–35, a₂₃ can now be calculated as follows:

(6–10)

The out-of-plane PPR was estimated as 0.698 from the 0° tension tests where strain was additionally measured in the through thickness direction.

Therefore from Equation 3–35, a₁₂ , and hence a₁₃ , can now be calculated as follows:

(6–11)

(6–12)

The a₄₄ plasticity coefficient was calibrated through simulation of the uniaxial tension test with loading at +/- 45° to the fibers. Using the plasticity coefficients derived so far in this section the quadratic yield function is sufficiently described to allow a₄₄ to be modified until the 45° tension test results were reproduced.

Best agreement with experiment is achieved with a₄₄ = 4.0 (see Figure 6.3: Results from Simulations of 45° Tension Tests. (Experimental Result Courtesy of EMI [2])).

Figure 6.3: Results from Simulations of 45° Tension Tests. (Experimental Result Courtesy of EMI [2])

In the absence of further experimental data it was assumed the out-of-plane shear plasticity coefficients are equal to the in-plane properties. Therefore,

(6–13)