標準面

最も一般的に使用される光学面は球面です。球面は現在の光軸の中心に配置され、頂点は現在の軸の位置にあります。OpticStudio では、平面を球面の特殊例 (曲率半径が無限の球面) として、コーニックを特殊例として処理します。標準面のサグ (z 座標) は、以下の式で求められます。

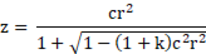
ここで c は曲率 (半径の逆数)、r は半径座標 (レンズ ユニット)、k はコーニック定数です。コーニック定数は、-1 より小さい場合は双曲線、-1 は放物線、-1 と 0 の間は楕円、0 は球面、0 より大きい場合は扁平楕円面を示します。

コーニック定数の詳細については「レンズ設計に関する参考文献」を参照してください。

標準面では、パラメータ列を使用しません。

標準面による楕円のモデリング

楕円面の長半径と短半径の長さを、半径とコーニックの記述に変換するために、いくつかの便利な式が用意されています。「a」が長半径の長さ、「b」が短半径の長さだとすると、以下のようになります。

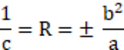
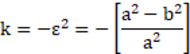
x 方向と y 方向で半軸長さが異なる楕円面については、「バイコーニック」を参照してください。

標準面によるアキシコンのモデリング

標準面を使用して、ほぼ完璧なアキシコンを作成できます。(1 + k) c² r² >> 1 の場合、標準面は次の式で記述できます。

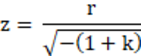
z = r tan(α) であることから、次のようになります。

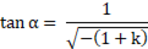
α は、XY 平面からアキシコン面までのアキシコン角です。アキシコンを作成するには、目的の角度 ( ) からコーニック定数値 (k) を計算し、曲率半径として任意の小さな値を使用します。k の結果値は負の数である必要があります。半径または曲率の正確な値は重要ではなく、アキシコンの半径アパチャーより、約 3 桁以上小さければ問題ありません。アキシコンは原点に値がないという意味では、完璧なものではありません。面の頂点の周囲の領域は、半径の値によっておおよそ指定されたサイズで丸められます。これは、実は光線追跡のためには望ましいプロパティです。面はどの部分も滑らかだからです。ただし、有効焦点距離や倍率などの一般的な 1 次光学特性をはじめとする近軸データは、一般的にアキシコン面では意味を持ちません。面の形状はコーニック非球面ですが、アキシコンの形状は、光学系の近軸特性が光学面全体を表現するものではないことを暗示しています。これは、曲率半径だけでは十分に説明できない光学面の例だと言えます。

次へ :

• スーパーコーニック