[ザイデル係数] (Seidel Coefficients)

ザイデル係数 (無変換、横、縦) と波面収差係数を表示します。

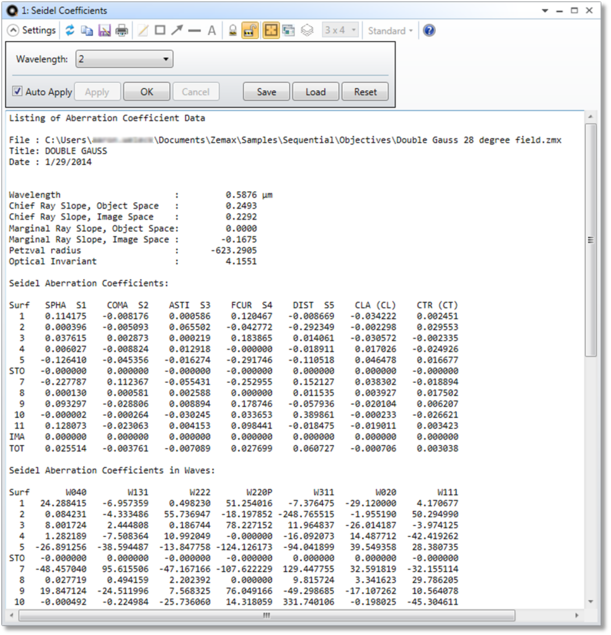
[波長] (Wavelength) 計算に使用する波長の番号です。

説明

OpticStudio では、未変換のザイデル係数、横収差係数、縦収差係数、およびいくつかの波面係数が計算されます。ザイデル係数は面ごとに表示され、また光学系全体での合計も表示されます。表示される係数は、球面収差 (SPHA、S1)、コマ収差 (COMA、S2)、非点収差 (ASTI、S3)、像面湾曲 (FCUR、S4)、歪曲収差 (DIST、S5)、縦色収差(CLA、CL)、および横色収差 (CTR、CT) です。単位は、波数を使用する係数を除き、必ず光学系のレンズユニットです。

これらの計算は、軸対称の球面、コーニック、2 次非球面、または 4 次非球面で構成する光学系でのみ有効で正確です。座標ブレーク、グレーティング、近軸面などの放射対称ではない面を持つ光学系は、これらの係数の計算に使用する近軸光線では十分に記述できません。具体的には、標準面、偶数次非球面、奇数次非球面、拡張非球面、および拡張奇数次非球面でこれらの係数を使用できます。

横収差係数は、各面および光学系全体について表示されます。計算される係数は、横球面収差 (TSPH)、横サジタルコマ収差 (TSCO)、横タンジェンシャルコマ収差 (TTCO)、横非点収差 (TAST)、横ペッツヴァール像面湾曲 (TPFC)、横サジタル像面湾曲 (TSFC)、横タンジェンシャル像面湾曲 (TTFC)、横ディストーション (TDIS)、横軸上色収差 (TAXC)、および横倍率色収差 (TLAC) です。横収差は光学系のレンズユニットで表示されます。横収差係数は、光線がほぼ平行光線となる光学空間ではきわめて大きくなることがあるので、そのような光学空間ではほとんど意味がありません。

ペッツヴァール和の逆数であるペッツヴァール曲率は次の式で表されます。

ここで、ni - 1 と ni は、面番号 i 前後の屈折率、Ri は面番号 i の曲率半径、nm は像面の屈折率、m は像面の面番号です。

ペッツヴァール曲率では、物空間と像空間の両方における屈折率の絶対値を考慮します。この計算では、物空間側と像空間側の曲率半径は無視されます。

縦収差係数は、縦球面収差 (LSPH)、縦サジタルコマ収差 (LSCO)、縦タンジェンシャルコマ収差 (LTCO)、縦非点収差 (LAST)、縦ペッツヴァール像面湾曲 (LPFC)、縦サジタル像面湾曲 (LSFC)、縦タンジェンシャル像面湾曲 (LTFC)、縦ディストーション (LDIS)、縦軸上色収差 (LAXC)、および縦倍率色収差 (LLAC) で計算されます。縦収差は光学系のレンズユニットで表します。縦収差係数は、光線がほぼ平行光線となる光学空間ではきわめて大きくなることがあるので、そのような光学空間ではほとんど意味がありません。

計算される波面係数は、球面収差 (W040)、コマ収差 (W131)、非点収差 (W222)、像面湾曲ペッツヴァール成分 (W220P)、ディストーション (W311)、軸上色デフォーカス項 (W020)、倍率色収差ティルト項 (W111)、像面湾曲サジタル成分 (W220S)、像面湾曲中間成分 (W220M)、および像面湾曲タンジェンシャル成分 (W220T) です。すべての波面係数は、射出瞳のエッジでの波長の単位で表されます。以下の表に示すように、さまざまな収差係数が互いに相関関係にあります。n’ および u’ の値は、それぞれ光学系の最終面での屈折率と近軸マージナル光線の角度です。ザイデル収差係数の意味と導出方法の説明については、『Aberrations of Optical Systems』 (Welford 著)、『Modern Lens Design』 (Smith 著)、または『Elements of Modern Optical Design』 (O' Shea 著) を参照してください。「レンズ設計に関する参考文献」に、優れた参考文献を一覧で挙げています。


名前	ザイデル	波	説明	横方向	縦方向
球面			球面
コマ収差			サジタル
コマ収差			タンジェンシャル
非点隔差			タンジェンシャル焦点からサジタル焦点へ
視野曲率			ガウシアンからペッツヴァールへ
			ガウシアンからサジタルへ
			ガウシアンからメディアルへ
			ガウシアンからタンジェンシャルへ
ディストーション			ディストーション
軸上色収差			色収差は、極値として定義した波長間で、選択した波長を基準として測定します。
倍率色収差			色収差は、極値として定義した波長間で、選択した波長を基準として測定します。