[ホイヘンス PSF] (Huygens PSF)

ホイヘンスのウェーブレット手法の直接積分を使用して、回折 PSF を計算します。ストレール比も計算されます。
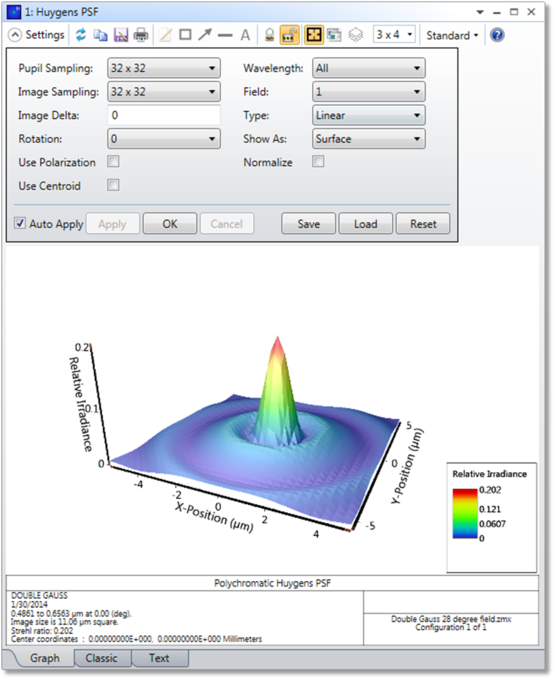
[瞳のサンプリング] (Pupil Sampling) 計算を実行するために追跡する光線のグリッド サイズを選択します。サンプリング密度が高いほど、より正確な結果が得られますが、計算時間も長くなります。
[像のサンプリング] (Image Sampling) 回折像の強度を計算する点グリッドのサイズ。この数値と像のデルタの組み合わせにより、表示される領域のサイズが決まります。
[像のデルタ] (Image Delta) 像グリッドでの 2 点間の距離 (マイクロメートル)。デフォルトのグリッド間隔を使用する場合は 0 を指定します。
[回転] (Rotation) 面プロットにどのように回転を適用するかを指定します。0、90、180、または 270°を選択できます。
[波長] (Wavelength) 計算に使用する波長の番号です。
[視野] (Field) 計算の対象となる視野の番号です。
[タイプ] (Type) 線形 (強度) または対数 (強度) を選択します。対数目盛は 10^1 ~ 10^5 の範囲で設定できます。振幅の実部、振幅の虚部、および位相 (°) も選択できます。線形振幅と複素振幅の関係については、以下の説明を参照してください。
[コンフィグレーション] (Configuration) すべてのコンフィグレーションで波長ごとに PSF のコヒーレントな合計を計算する [全て] (All)、[現在] (Current)、またはいずれかのコンフィグレーションを選択します。このオプションでは、コンフィグレーションごとに同じ波長の PSF をコヒーレントに加算した後、得られた PSF を波長別にインコヒーレントに加算します。このため、定義されている各波長がすべてのコンフィグレーションで同じであることが必要です。波長とコンフィグレーションに重み付けを適用することもできますが、同じ波長を使用している必要があります。「マルチコンフィグレーション オペランドの概要」で CWGT および WLWT を参照してください。このコヒーレントな加算では、すべてのコンフィグレーションで像面が同じ位置にあることも前提となります。[全て] (All) を選択した状態で、フォーカル モードとアフォーカル モードの両方のコンフィグレーションを定義している場合、[コンフィグレーション] (Configuration) の設定は自動的に [現在] (Current) にリセットされます。
[正規化] (Normalize) チェックすると、ピーク強度が 1 で正規化されます。チェックをはずすと、ピーク強度は、収差のない PSF (ストレール比) のピーク値で正規化されます。
[表示方法] (Show As) 表示オプションとして、面のプロット、輪郭マップ、グレー スケール、または疑似カラー マップを選択します。[トゥルー カラー] (True Color) オプションでは、各波長をそれに最も近い RGB に変換し、すべての波長にわたって加算することにより、RGB 色による PSF の表現を作成します。トゥルー カラー表現の精度はコンピュータのディスプレイ上での色の RGB レンダリング手法により制限されます。また単色を正確に表現することはできません。[タイプ] (Type) が線形以外の場合は [トゥルー カラー] (True Color) オプションを使用できません。[トゥルー カラー] (True Color) を選択すると、データの再計算が必要になります。RGB への変換は、PSF とは無関係な方法で計算されるからです。他の表示オプションでは再計算は不要です。
[偏光を使用] (Use Polarization) チェックすると、偏光が考慮されるようになります。偏光の状態を定義する方法と解析機能での偏光の使用方法については「[偏光] (Polarization) (システム エクスプローラ)」を参照してください。
[セントロイドを使用] (Use Centroid) チェックすると、幾何光学的な像のセントロイドを中心としてプロットが表示されます。チェックをはずすと、主光線を中心として表示されます。
説明 :
回折の影響を検討する方法として、波面上の各点を振幅と位相を持つ完全な点光源として考える方法があります。これらの各点光源は、球面状の「ウェーブレット」 (最初にこのモデルを提案したホイヘンスの名を取って「ホイヘンス ウェーブレット」と呼ぶこともあります) を放射します。空間を伝搬する波面の回折は、放射されるすべての球面状ウェーブレットの干渉、つまり複素和により得られます。
ホイヘンス PSF を計算するには、光学系の中を伝搬する光線のグリッドを送出して、それらの光線ごとに特定の振幅と位相のウェーブレットを表現するようにします。像面上の任意の点での回折強度は、これらすべてのウェーブレットの複素和を二乗した値になります。像グリッド上の各点で、PSF がこの方法で計算されます。グラフとテキストの両方で示される中心座標は、[セントロイドを使用] (Use Centroid) をチェックしている場合、ビームの幾何学的セントロイドで定義されます。[セントロイドを使用] (Use Centroid) をチェックしていない場合は、PSF の計算位置となった視野点の主光線に相当します。グラフは、必ずこの中心座標である (n/2+1), (n/2+1) を中心とした表示になります。n は、像空間グリッドにある点の数です。回転対称光学系のデータ出力は、点 (n/2, n/2+1) を中心として対称になります。これとは別に、[セントロイドを使用] (Use Centroid) をチェックしているかどうかに関係なく、OpticStudio では、中心座標とホイヘンス PSF 自体のセントロイド位置との偏差が必ず計算されます。この PSF のセントロイドは、PSF の 2 次モーメント解析から求めます。この偏差は、セントロイドのオフセットとしてテキストに示されます。これにより、中心座標にセントロイドのオフセットを加算した値がセントロイドの座標としてテキストに示されます。
[像のデルタ] (Image Delta) 値は、像空間グリッドの点間隔を指定します。値 0 を指定すると、デフォルトのグリッド間隔が使用されます。デフォルトの像のデルタは、以下の式で求められます。
np は瞳空間グリッドにある点の数、λ は設定で選択した波長、F は実効 F ナンバーです。[波長] (Wavelength) の設定が [全て] (All) である場合、λは定義された波長のうち最長です。PSF の全幅が n × (像のデルタ) の範囲内にあれば、像のデルタ サイズの厳密な値は重要ではありません。
FFT PSF と異なり、ホイヘンス PSF は、主光線の交差位置で像面に接している虚数平面上で計算されます。この虚数平面は、主光線に垂直ではなく、目的の面の法線に対して垂直です。したがって、ホイヘンス PSF では、像面の傾斜と主光線の入射角のいずれかまたはその両方によって発生する像面の局所的なティルトが考慮されます。
ホイヘンス手法では、像面に沿ったビームの伝搬に伴って変化する回折像の形状も考慮されます。像面が入射ビームに対してティルトしている場合、この機能には重要な効果があります。ホイヘンス PSF 手法のもう 1 つの利点として、あらゆるグリッド サイズと間隔を選択できるということがあります。これにより、F ナンバーや波長が異なっていても、2 つの異なるレンズによる PSF を直接比較できます。
ホイヘンス PSF の唯一の欠点は速度です。FFT 手法と比較すると、直接積分は低速になります (詳細については、前の節を参照してください)。計算時間は、瞳グリッド サイズの二乗×像グリッド サイズの二乗×波長数によって決まります。OpticStudio では、光学系の対称性も考慮されます。ホイヘンス PSF では、可能な限りの高速演算を実現するために、複数の CPU を搭載したコンピュータでは使用可能なすべてのプロセッサが自動的に使用されます。
一般的に、ホイヘンス PSF の構築時には、位相の計算に平面基準を使用します。遠方の瞳から光線が出発していると見なすことができる場合、および対象とする像の領域が小さい場合は、この基準を問題なく使用できます。この基準の適用により、瞳からの光線はすべて平面波として扱うことができます。平面波では平面全体で位相が一定であることから、像にある 1 つのピクセルの中心に到達した平面波の位相は、平面波からピクセルまでの距離に 2π/λを乗じた値を光線の位相に加算した値になります。個々の光線に相当する各平面波をすべてコヒーレントに合算するとホイヘンス PSF が得られます。
一方、像が大きい場合は、瞳での光線位置から各ピクセルまでの距離が光線位置によって大きく異なるので、平面波の近似を使用できなくなります。近似の使用可否は、射出瞳から像の中心までの距離と射出瞳から像の縁までの距離を計算することで判断できます。これら 2 つの距離の差が 1/4 波長より大きい場合は、像の位相湾曲量が無視できなくなるため、平面波では光学系を正しく近似できなくなります。その場合は、位相基準として球面波が使用されます。球面波基準の使用によって、ホイヘンス PSF の計算時間が長くなることがあります。これは、ピクセルごとに位相を計算する必要があり、ピクセル座標と位相との線形関係を前提とすることができなくなるからです。一方で、像面に顕著な収差が存在し、平面波基準を使用するとノイズの多い結果が得られる光学系では、はるかに高精度な PSF が得られます。このように必要に応じて球面波の基準を使用できることから、ホイヘンス PSF は広範な光学系に適用できます。たとえば、コンピュータ生成のホログラムをモデル化する光学系があります。
OpticStudio では、ホイヘンス積分の射出瞳に適用する位相基準を平面波とするか球面波とするかを、上記の判断基準に従ってデフォルトで自動的に判断します。
この自動判定を無効にして手動で基準を設定するには、システム エクスプローラの [ホイヘンス積分の計算方法] (Method to Compute Huygens Integral) オプションの選択を変更します ([設定] (Setup) タブ→ [システム] (System) グループ → [システム エクスプローラ] (System Explorer) → [上級] (Advanced))。
線形 PSF (光束単位) と、「実数 PSF + i* 虚数 PSF」として定義され、フィールドまたは sqrt(光束) の単位を持つ複素振幅の間の基本的な関係は、「線形 PSF = (実数 PSF) ^2 + (虚数 PSF)^2」 として与えられます。)線形量、実数、虚数のホイヘンスの和はすべて個別に累積されるため、それらの値は瞳孔と像のサンプリングに関してわずかに異なるレートで収束する可能性があります。
多色 PSF を実行する場合、波長ベースの係数「wFactor」が線形 PSF タイプに適用されることに注意してください。この係数の目的は、多色 PSF に対するさまざまな波長の寄与を重み付けすることです。wFactor は次のように指定されます。
一方、ω-multi はマルチコンフィグレーション エディターからの CWGT オペランドの値によって与えられ、ω-wave は波長設定からの波長の重みです。
複数のコンフィグレーションにわたる偏光および PSF の合計に関するコメント
さまざまなコンフィグレーションのビームが直交していて、強く偏光している場合は、ホイヘンス PSF に正確な結果が得られるように入力偏光を考慮する必要があります。システム エクスプローラで [無偏光] (Unpolarized) 設定のチェックをはずし、ホイヘンス PSF のプロパティで [偏光を使用] (Use Polarization) をチェックします。システム エクスプローラで変更を設定する方法の詳細については「[偏光] (Polarization) ([システム エクスプローラ] (System Explorer))」を参照してください。
ホイヘンス PSF の設定で [偏光を使用] (Use Polarization) をチェックしていても、システム エクスプローラで [無偏光] (Unpolarized) をチェックしたままにしていると、ホイヘンス PSF の結果が不正確になることがあります。このような設定で複数のコンフィグレーションにわたって PSF を合算すると、コンフィグレーションごとに平均の偏光透過が計算され、ここで得られたエネルギーが、透過電場の x 成分に割り当てられます。これらのコンフィグレーションに対して得られたエネルギーは人為的にこの状態に置かれるので、ホイヘンス PSF ではコヒーレントに合算されます。しかし、直交偏光はコヒーレントに干渉しないので、さまざまなコンフィグレーションのビームが直交していて、強く偏光している場合、この結果は不正確なものになります。このような状態を避けるには、システム エクスプローラで [無偏光] (Unpolarized) のチェックをはずします。これにより、正しい偏光ビーム入力が使用されるようになります。
次へ :


