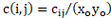チェビシェフ多項式
チェビシェフ多項式面は、基本の曲率半径と一連のチェビシェフ多項式で記述できるフリーフォーム面です。一次元の第一種チェビシェフ多項式は、以下の式で表されます。

参考として、チェビシェフ多項式の低次側 10 項の係数を以下に示します。
T0 (x) = 1
T1 (x) = x
T2 (x) = 2x2 – 1
T3 (x) = 4x3 - 3x
T4 (x) = 8x4 - 8x2 + 1
T5 (x) = 16x5- 20x3 + 5x
T6 (x) = 32x6 - 48x4 + 18x2 – 1
T7 (x) = 64x7 - 112x5 + 56x3 - 7x
T8 (x) = 128x8 - 256x6 + 160x4 - 32x2 + 1
T9 (x) = 256x9 - 576x7 + 432x5 - 120x3 + 9x
T10 (x) = 512x10 - 1280x8 + 1120x6 - 400x4 + 50x2 - 1
二次元チェビシェフ多項式にするには、積の基底 tij(x,y) を使用します。
OpticStudio では、x と y の最大次数は 14 に設定されます。どの関数もチェビシェフ多項式の項の有限和として補間できます。
2D チェビシェフ多項式の引数は、単位間隔で定義されます。任意の間隔の補間を有効にするには、多項式の引数として正規化したと
を使用します。
チェビシェフ多項式面のサグ (z 座標) は、以下の式で求められます。
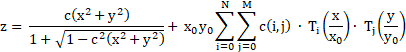
c は面の頂点における曲率、および
は正規化長さ、
は正規化された多項式係数で、
が成り立ちます。
正規化半径である X0 と Y0 の外側ではチェビシェフ面が定義されません。正規化半径の外側でチェビシェフ面に到達する光線は追跡できず、そのチェビシェフ面でビネッティングされます。
チェビシェフ多項式面のパラメータ定義
| パラメータ番号 | 名前 | 定義 |
| 1 | 最大 X 次数 | X 座標の多項式の最大次数 (整数、最大 14 次) |
| 2 | 最大 Y 次数 | Y 座標の多項式の最大次数 (整数、最大 14 次) |
| 3 | X 方向の正規化長さ |
正規化長さ |
| 4 | Y 方向の正規化長さ |
正規化長さ |
| 13 ~ 236 |
|
正規化された多項式係数 |
次へ :