Axicon Surface

There are many types of axicons. Common polynomial types can be modeled using the Aspheric Surface (see " Aspheric Surface " ).
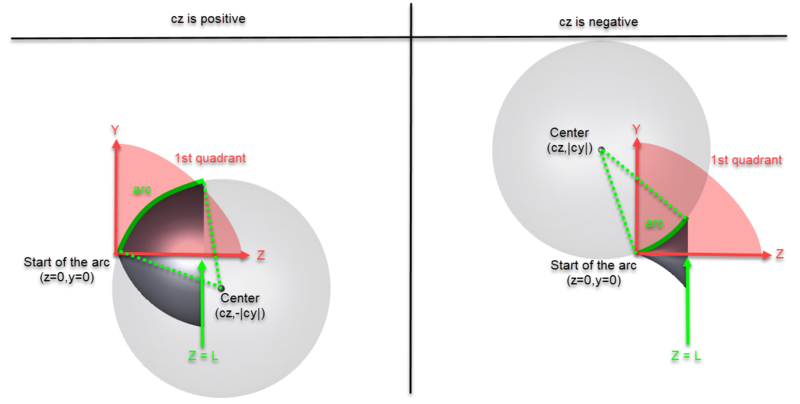
The Axicon Surface object uses a different method for defining the object shape. The Axicon surface is defined by a section of a circle (an arc) that lies in the YZ plane. The arc is defined by three points. The start of the arc is at (z=0, y=0). The center of the arc is at the user defined coordinates (cz, cy). The end of the arc is at the point where z = L, where L is a user defined parameter corresponding to the length of the axicon along the Z axis. The surface is formed by revolving the arc around the Z axis. If cz is positive, the negative of the absolute value of cy is taken, and the portion of the circle lying in the first quadrant is used to define the surface. If cz is negative, the absolute value of cy is taken, and the portion of the circle lying in the first quadrant is used to define the surface.
The following parameters are used to define the axicon surface:
| Parameter # | Description | Face Name | Face # |
| 1 | The length of the axicon along the local z axis. | All Faces | 0 |
| 2 | The z coordinate of the center of the arc measured in the YZ plane. | All Faces | 0 |
| 3 | The y coordinate of the center of the arc measured in the YZ plane. | All Faces | 0 |
Face Numbers: All faces Face 0.
Next:


