Aspheric Surface

An aspheric surface is defined by the following sag equation:
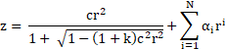
where c is the curvature of the surface, k is the conic constant, r is the radial coordinate, and the α terms are aspheric coefficients. The surface supports specification of both a minimum and a maximum radial aperture; so annular surfaces may be defined. Note that both even and odd terms are defined; up to approximately 240 coefficients may be used.
The following parameters are used to define the aspheric surface:
| Parameter # | Description | Face Name | Face # |
| 1 | The radius of curvature. If this value is zero, then the curvature is assumed to be zero. | All Faces | 0 |
| 2 | The conic constant k. | All Faces | 0 |
| 3 | The maximum radial aperture in lens units. | All Faces | 0 |
| 4 | The minimum radial aperture in lens units. This value may be zero. | All Faces | 0 |
| 5-6 | Unused. | All Faces | 0 |
| 7 | The number of terms to use in the aspheric expansion. Ray tracing will be faster if this term is no larger than the highest order non-zero coefficient. | All Faces | 0 |
| 8-249 | The α coefficients on the polynomial expansion. | All Faces | 0 |
Face Numbers: All faces Face 0.
This object supports user defined apertures, see " User defined apertures ". For other aperture shape options, see " Aspheric Surface 2 ".
Next:


