Setting Up Nonlinear Programming by Quadratic Lagrangian (Gradient) Optimizer

Follow this procedure to set up an optimization analysis using the Nonlinear Programming by Quadratic Lagrangian (Gradient) Optimizer. Once you have created a setup, you can Copy and Paste it, then make changes to the copy, rather than redoing the whole process for minor changes.

The NLPQL (Nonlinear Programming by Quadratic Lagrangian) method can be used for Direct Optimization systems. It lets you generate a new sample set to provide a more refined approach than the Screening method. Available for continuous input parameters only, NLPQL can handle only one output parameter goal. Other output parameters can be defined as constraints. For more information, see Convergence Rate % and Initial Finite Difference Delta % in NLPQL and MISQP and Nonlinear Programming by Quadratic Lagrangian (NLPQL).

To generate samples and perform an NLPQL optimization:

1. Set up the variables you want to optimize in the Design Properties dialog box. The variables must be swept in a Parametric setup.
2. Click HFSS or Q3D Extractor or 2D Extractor > Optimetrics Analysis > Add Screening & Optimization . The Setup Optimization dialog box appears.

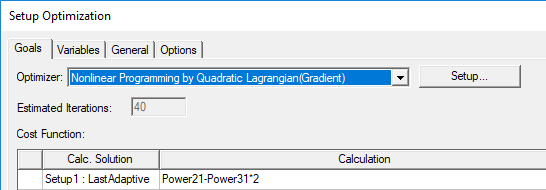
3. Under the Goals tab, select the optimizer by selecting Nonlinear Programming by Quadratic Lagrangian (Gradient) from the Optimizer drop-down list.

4. Optionally, click Setup to open the Optimizer Options dialog box.
   
   

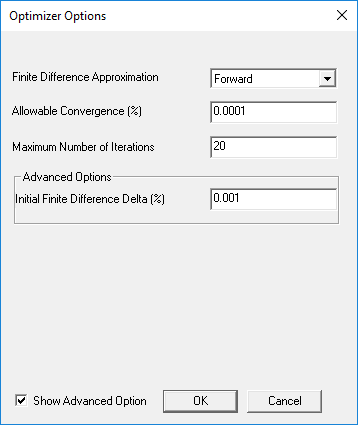
• Finite Difference Approximation – When analytical gradients are not available, NLPQL approximates them numerically. This property lets you specify the method of approximating the gradient of the objective function. Choices are:
• Central – Increases the accuracy of the gradient calculations by sampling from both sides of the sample point, but increases the number of design point evaluations by 50%. This method makes use of the initial point, as well as the forward point and rear point.
• Forward – Uses fewer design point evaluations, but decreases the accuracy of the gradient calculations. This method makes use of only two design points, the initial point and forward point, to calculate the slope forward. This is the default method for new Direct Optimization systems.
• Maximum Number of Iterations – Stop criterion. Maximum number of iterations that the algorithm is to execute. If convergence happens before this number is reached, the iterations stop. This also provides an idea of the maximum possible number of function evaluations that are needed for the full cycle. For NLPQL, the number of evaluations can be approximated according to the Finite Difference Approximation gradient calculation method, as follows:
• For Central: number of iterations * (2*number of inputs +1)
• For Forward: number of iterations * (number of inputs+1)
• Allowable Convergence (%) – Stop criterion. Tolerance to which the Karush-Kuhn-Tucker (KKT) optimality criterion is generated during the NLPQL process. A smaller value indicates more convergence iterations and a more accurate (but slower) solution. A larger value indicates fewer convergence iterations and a less accurate (but faster) solution. For a Direct Optimization system, the default percentage value is 0.1. The maximum percentage value is 100. These values are consistent across all problem types because the inputs, outputs, and gradients are scaled during the NLPQL solution.

• Initial Finite Difference Delta (%) – Advanced option for specifying the relative variation used to perturb the current point to compute gradients. Used in conjunction with Allowable Convergence (%) to ensure that the delta in NLPQL's calculation of finite differences is large enough to be seen above the noise in the simulation problem. This wider sampling produces results that are more clearly differentiated so that the difference is less affected by solution noise and the gradient direction is clearer. The value should be larger than both the value for Initial Finite Difference Delta (%) and the noise magnitude of the model. However, smaller values produce more accurate results, so set Initial Finite Difference Delta (%) only as high as necessary to be seen above simulation noise.

• The default percentage value is 1. The minimum is 0.0001, and the maximum is 1. For parameters with Allowed Values set to Manufacturable Values or Snap to Grid, the value for Initial Finite Difference Delta (%) is ignored. In such cases, the closest allowed value is used to determine the finite difference delta.

5. Add a cost function - Click Setup Calculations to open the Add/Edit Calculation dialog box.

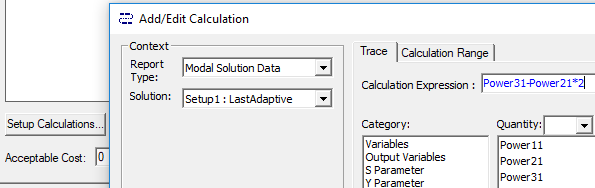
When you have created the calculation, click Add Calculation to add it to the Optimization setup, and Done to close the Add/EditCalculation dialog box.

6. In the Optimization setup, in the drop-down list for the Goal column, select Edit as Expression or Edit as Numeric Value.



7. This reopens the Add/Edit Calculation dialog box. If you are satisfied with the expression or value displayed, click Done to close the dialog box. This enters the expression/value to the Goal column.
   
8. In the Optimization setup, if you want to select a Cost Function Norm Type:

• Select the Show Advanced Option check box. The Cost Function Norm Type drop-down list appears.

• Select L1, L2, or Maximum.

A norm is a function that assigns a positive value to the cost function.

For L1 norm the actual cost function uses the sum of absolute weighted values of the individual goal errors. For L2 norm (the default) the actual cost function uses the weighted sum of squared values of the individual goal error. For the Maximum norm the cost function uses the maximum among all the weighted goal errors, which means that it is always less than zero. (For further details, see Explanation of the L1, L2, and Max Norms in Optimization.)

The norm type doesn't impact goal setting that use as condition the "minimize" or "maximize" scenarios.

9. Optionally, set the Acceptable Cost and Cost Function Noise.
10. Optionally, click HPC and Analysis Options to select or create an analysis configuration.
11. In the Variables tab, specify the Min/Max values for variables included in the optimization.

• You can also override the variable starting values by selecting the Override check box and entering the desired value in the Starting Value field.
• Optionally, modify the values of fixed variables that are not being optimized.
• Optionally, set Linear constraints.
• Select the View all columns check box to see all columns, including hidden columns.

12. In the General tab, specify whether Optimetrics should use the results of a previous Parametric analysis or perform one as part of the optimization process.

    Select the Update design parameters' value after optimization check box to cause Optimetrics to modify the variable values in the nominal design to match the final values from the optimization analysis.

13. Under the Options tab, if you want to save the field solution data for every solved design variations in the optimization analysis, select Save Fields And Mesh.
    Note:

    Do not select this option when requesting a large number of iterations as the data generated will be very large and the system may become slow due to the large I/O requirements.

You may also select Copy geometrically equivalent meshes to reuse the mesh when geometry changes are not required, for example when optimizing on a material property or source excitation. This will provide some speed improvement in the optimization process.

Related Topics 

Convergence Rate % and Initial Finite Difference Delta % in NLPQ and MISQP