Formulation of the DC Conduction Solution

Any object that has been identified as a conductor is included in the conduction simulation. The current density 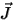in each conductor is, by Ohm 's law, proportional to the electric field that results from gradients in the electrostatic potential Φ:

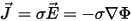
where σ is the conductivity of the material.

Under steady state DC conditions, the amount of charge leaving any infinitesimally small region must equal the charge flowing into that region. That is, the charge density, ρ (x,y,z), in any region will not change with time:

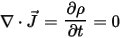
Therefore Q3D must find a solution to the equation:

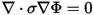
This is one form of Laplace 's equation. The conduction solver uses the finite element method with quadratic basis functions to compute the potential at each vertex and edge midpoint in the mesh. The finite element matrix is solved using a direct solver that exploits the sparsity of the linear system of equations. The boundary conditions that must be applied are:

• The normal component of the current density must be zero at an interface between the conductor and an insulating region, such as a dielectric or free space.
• The electrostatic potential must be continuous across an interface between two conductors.
• The electrostatic potential on a source or sink terminal is constant (equipotential) over the terminal surface, and the total current is equal to the externally applied source.