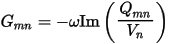Extracting Capacitance and Conductance from the Charge Solution

From circuit theory, it is known that the current I across the parallel combination of a conductance G and a capacitance C excited by a voltage V is given by

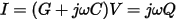
Here ω is the angular frequency, and we have made use of the fact that the current is the time derivative of the charge on the circuit node, Q. This implies that we can extract the conductance and capacitance if we know the total charge on the conductor and the applied voltage using the formula:

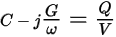
By matching the real and imaginary parts on both sides of this equation, we get separate expressions for the capacitance and conductance:

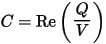
and

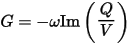
Q_mn

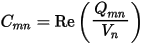
and