Formulation of the Capacitance/Conductance Solution

The electrostatic potential Φ produced by a distribution of charges ρ on a surface S is given by the integral equation

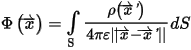
Here the operator || || denotes the Euclidean length of a vector. The equation is based upon an implicit assumption that the potential will go to zero as the distance between the source and observation points goes to infinity. This assumption can be relaxed by applying the Floating at Infinity matrix reduction operation as a post-processing step.

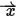
If dielectric objects are present in the problem, they must also be taken into account. The electromagnetic boundary condition at the interface between two dissimilar dielectrics is the continuity of the normal electric flux:

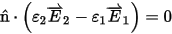
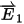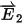Here n̂ is the unit vector normal to the dielectric interface. The dielectric constants ε₁ and ε₂ on opposite sides of the interface are real-valued for lossless dielectrics and complex-valued (and possibly frequency-dependent) for lossy dielectrics. and are the corresponding electric field vectors.

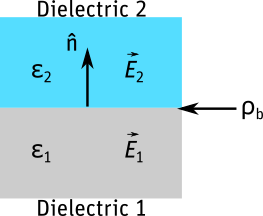
ρ_b

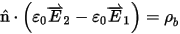
Because the electric field appearing in this equation is the negative of the gradient of the electrostatic potential Φ, it can be found by carefully differentiating the equation. The bound charge density ρ_b appearing in the equation constitutes an additional set of field sources that must be computed by the solver. Q3D creates additional mesh triangles on the dielectric interface and solves for the bound charge densities in these triangles, iteratively updating them until all conditions are satisfied.