Defining Anisotropic Relative Permeability Tensors
Eddy or Frequency Domain Solutions Only
The relative permeability of materials is assumed to be a complex quantity expressed as the following:
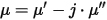
where µ' is the real part of the complex permeability (same as the usual relative permeability), µ" is the imaginary part of the complex permeability, and j is the imaginary unit.
The relationship above can also be written as the following:
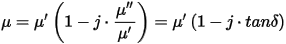
where tand is the magnetic loss tangent.
For anisotropic magnetic materials, a tensor material property needs to be used. The anisotropic relative permeability tensor has the following expression:
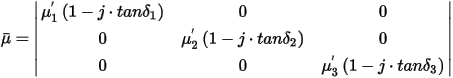
Magnetostatic, Eddy, and Transient Solutions Only
Maxwell allows the anisotropic magnetic material to exhibit nonlinear characteristics (magnetostatic, Eddy, and transient solutions only) on all three principle axes of the chosen coordinate system, in which case the respective nonlinear characteristics must be specified.
For example, for laminations with anisotropic behavior in the plane of the lamination, the Anisotropic type of material should be specified for the Relative Permeability property, and the two respective B-H curves should be entered. For the third direction (lamination stacking direction), one of the specified two B-H curves should also be applicable. The composition field should be set to lamination, and the stacking factor and stacking direction should be specified (see also lamination model).
General
If the material property is anisotropic, its characteristics are defined by its anisotropy tensor. You must define three diagonals for anisotropic permeability. Each diagonal represents a tensor of your model along an axis.
These tensors are relative to the coordinate system specified as the object’s Orientation property. By specifying different orientations, several objects can share the same anisotropic material but be oriented differently.
- In the Relative Permeability row in the View/Edit Material window, select Anisotropic from the Type drop-down menu.
- Enter the relative permeability along one axis of the material’s permeability tensor in the Value box of the T(1,1) row.
- Enter the relative permeability along the second axis in the Value box of the T(2,2) row.
- Enter the relative permeability along the third axis in the Value box of the T(3,3) row.
Three rows named T(1,1), T(2,2) and T(3,3) are added below the Relative Permeability row.
If the relative permeability is the same in all directions, use the same values for each axis.
These values can also be defined as variables.
Related Topics
Creating a Relative Coordinate System
Change the Orientation of an object
Defining Anisotropic Relative Permittivity Tensors
Defining Anisotropic Conductivity Tensors
