HFSS Setup: Options Tab

Select the Options tab of the HFSS Setup window to access the following settings.

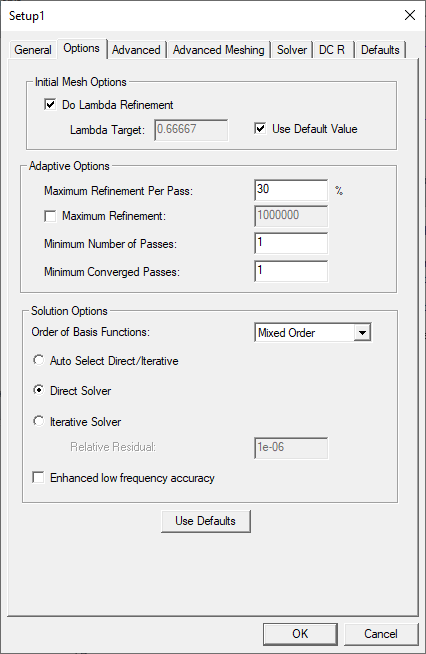
Initial Mesh Options: options that define the initial mesh before adaption.

• Do Lambda Refinement: Lambda refinement is the process of refining the initial mesh based on the material-dependent wavelength.
• Lambda Target: The fraction of the wavelength that determines the refined tetrahedra edge length (e.g., if the value is 0.1 then a edge length of 0.1 is used as the refinement target).
• Use Default Value: The target defaults depend on the Order of Basis function selections (e.g., for Driven solutions and a First Order basis function, the default target is 0.3333; HFSS refines the mesh until most element lengths are approximately one-third wavelength.).

Adaptive Options:

• Maximum Refinement Per Pass: determines how many tetrahedra are added at each iteration of the adaptive refinement process. The tetrahedra with the highest error is refined. The value is a percentage.
• Maximum Refinement: The maximum number of tetrahedra that can be added during an adaptive pass. By default, this unchecked, to there is no maximum. If you enable the Maximum Refinement, the initial value is 1000000.
• Minimum Number of Passes: The maximum number of mesh refinement cycles that you want HFSS to perform. This value is a stopping criterion for the adaptive solution. If the maximum number of passes has been completed, the adaptive analysis stops. If the maximum number of passes has not been completed, the adaptive analysis continues unless the convergence criteria are reached.
• Minimum Converged Passes: An adaptive analysis does not stop unless the minimum number of converged passes has been completed. The convergence criteria must be met for at least this number of passes before the adaptive analysis stops.

Solution Options:

• Order of Basis Functions: The order of the basis functions HFSS uses to interpolate field values from nodal values. The Zero order option is useful when a model requires a mesh that produces more than 100,000 tetrahedra, but the model size is small compared to wavelength. The higher order options solve progressively more unknowns for each tetrahedra. Mixed order uses higher order where more accuracy is required, and lower order where fields are weaker.
• Auto Select Direct/Iterative: The auto solver automatically chooses whether to use the direct (i.e., default) or iterative solver for each pass. The direct solver provides a multi-frontal (MF) approach and is invoked by default if the matrix is not well-conditioned for an iterative solution. The iterative solver significantly reduces memory usage, and it can also reduce solution time for large simulations.
• Enable Direct Solver (i.e., default): The direct solver is a multi-frontal solver ideal for smaller simulations.
• Enable Iterative Solver: The iterative solver provides an alternative to the multi-frontal solver when a matrix is well-conditioned for an iterative solution. The iterative solver significantly reduces memory usage, and it can also provide a savings in the solution time for large simulations. When this option is enabled, HFSS automatically invokes the iterative solver when it decides the matrix is conditioned well enough to take advantage of the iterative approach. HFSS uses the multi-frontal solver if the matrix does not meet this requirement.
• Relative Residual: The residual measures the convergence of the iterative solver. The default value is 1E-4.
• Enhanced low frequency accuracy: When enabled, the solver is tuned to reliably solve low frequencies for designs that only contain lumped ports as sources or a combination of lumped and circuit ports. For designs with only lumped ports and/or circuit ports, interpolating sweeps are tuned to solve more low frequency points in order to accurately represent very low frequency results.
  Important:

  Enhanced low frequency accuracy has no affect on Discrete sweeps.

  Note:

  Enhanced low frequency accuracy does not support wave ports at this time.

  Note:

  Enhanced low frequency accuracy requires more RAM in order to solve the entire solution vector for interpolation sweeps and for discrete sweeps not saving fields. For more information, see Horizontal Lumped Ports.