The ability to predict separation depends mostly on the level of the eddy-viscosity in the boundary layer. A suitable approach for tuning the model to adverse pressure gradients and separation is to allow a re-calibration of the basic model constants, while at the same time maintaining the calibration for the slope of the logarithmic layer and the proper near wall viscous damping required for achieving the correct shift in the log-layer (and thereby the correct wall shear stress). This is achieved by using the free parameter .

Figure 12.172: Change of the eddy-viscosity ration (EVR) under changes of for a flat plate. Top:=1.0 (all else default). Bottom =1.75 (all else default) shows the effect of on a flat plate boundary layer computation for the ratio . Increasing from =1.00 to =1.75 leads to a significant reduction in the ER levels. (Note that the effect is even more pronounced for flows with adverse pressure gradients and separation).

Figure 12.172: Change of the eddy-viscosity ration (EVR) under changes of for a flat plate. Top:=1.0 (all else default). Bottom =1.75 (all else default)

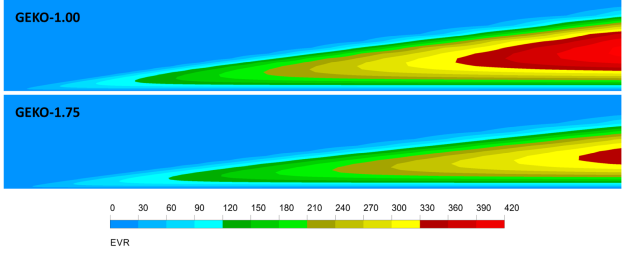
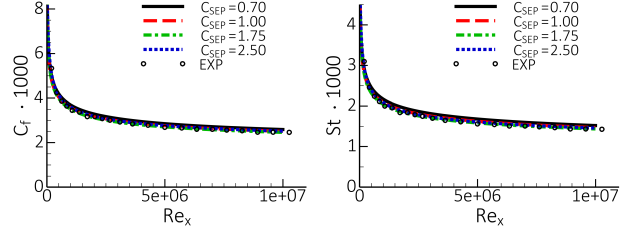
Figure 12.173: Flat plate boundary layer under variation of (=0.5). Left: Wall-shear stress coefficient, , Right: Wall heat transfer coefficient, St shows that even large changes in do not have any effect on the wall shear stress () and heat transfer coefficients (St). This is the basic design criterion for the GEKO model. It ensures that the user can adjust coefficients like freely (within range).

Figure 12.173: Flat plate boundary layer under variation of (=0.5). Left: Wall-shear stress coefficient, , Right: Wall heat transfer coefficient, St

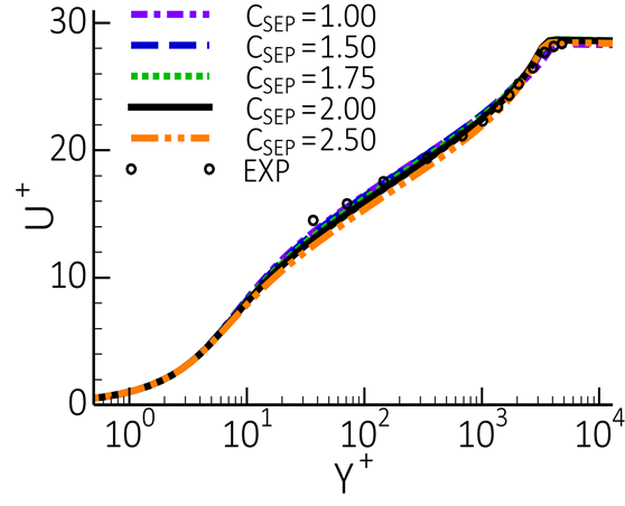
The independence of the mean flow velocity is also illustrated by the logarithmic velocity profiles shown in Figure 12.174: Velocity profiles in logarithmic plot under variation of for flat plate. Again, the logarithmic velocity profile is maintained over a wide range of coefficients.

Figure 12.174: Velocity profiles in logarithmic plot under variation of for flat plate

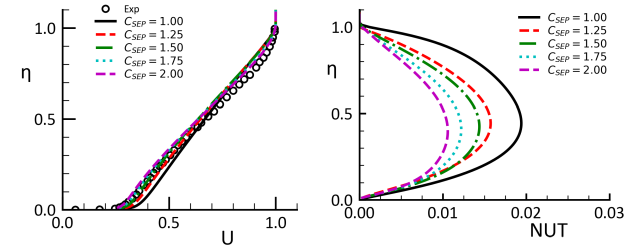
The effect of on an equilibrium adverse pressure-gradient boundary layer flows is demonstrated for the experiment of Skare and Krogstad () [21]. The simulations are based on the equilibrium boundary layer equations as given by Wilcox [31]. The non-dimensional pressure gradient drives the flow close to separation, a regime, which is very sensitive to turbulence modeling. The left part of Figure 12.175: Impact of variation in on boundary layer with adverse pressure gradient. Left: Velocity profile. Right Eddy-viscosity profiles shows the influence of on the velocity profiles whereas the right part shows the impact on the non-dimensional eddy-viscosity, ( is the velocity at the edge of the boundary layer and is the displacement thickness). The velocity profile exhibits moderately but visibly more decelerated with increasing . The eddy-viscosity, however, is drastically reduced by more than a factor of two by the variation of between 1-2. The most accurate solution is the one with =1.75. This reduction in eddy-viscosity is desirable for adverse pressure-gradient boundary layers, as low values increase the sensitivity of the model to adverse pressure gradients and separation. Note that the coefficients , have little effect on the boundary layer flows, due to the blending function being mostly equal to one inside the boundary layer. The parameter was set to its default value =0.5 (as will be detailed later). However, variations of would have little effect on the current flow.

Figure 12.175: Impact of variation in on boundary layer with adverse pressure gradient. Left: Velocity profile. Right Eddy-viscosity profiles

The effect of variation in is shown in Figure 12.176: Impact of variation in on CS0 diffuser flow [10]. Left wall shear stress coefficient, . Right: Wall pressure coefficient for the axi-symmetric diffuser flow of Driver et al [10] (=0.5, =CMixCor, =0.9). As expected from the results for the equilibrium boundary layer, with increasing , the model becomes more sensitive to the adverse pressure gradient in the diffuser and improves its separation predict up to a value of ~1.75-2.00. Higher values of lead to over-separation. Note that an optimal calibration of a turbulence model for the CS0 diffuser, does not necessarily guarantee an optimal solution for other similar flows. As will be shown below, for 2D airfoils more 'aggressive' settings are required to match the exp. data. It is therefore desirable that the GEKO model can be pushed to over-separation for the CS0 case.

Figure 12.176: Impact of variation in on CS0 diffuser flow [10]. Left wall shear stress coefficient, . Right: Wall pressure coefficient

Figure 12.177: Impact of variation in on velocity profiles for CS0 diffuser flow [10]

A more realistic application for tuning the coefficient is the simulation of 2D airfoil profiles under variation of the angle of attack, . Figure 12.178: Prediction of lift and pressure coefficients with GEKO model for DU-96-W-180 (Left) and DU-97-W-300 (Right) airfoil at [28] to Figure 12.182: Prediction of lift coefficient in wide range of angle of attacks (Left) and pressure coefficient for (Right) with GEKO model for S814 airfoil at [26] compare lift curves for numerous airfoils computed with the GEKO model. In these comparisons, it should be kept in mind that 2D simulations are not entirely correct in the stall and post-stall region (around and past maximum lift, ), due to the formation of 3D structures in the experiments. Despite of this, it is possible to adjust the GEKO model for the prediction of such flows for angles of attack in 2D simulations. Increasing predicts earlier separation onset, which improves agreement of the predicted pressure coefficient and results in an improved agreement of the lift coefficient with the experimental data^[5] near stall. The optimal value for for such flows is therefore somewhere between =2.00-2.50.

The current test cases demonstrate the advantage of the GEKO model over e.g. the SST model. The SST model is tuned to match adverse pressure gradients flows and flows with separation well on average. However, for the 2D airfoils the SST model is clearly too conservative resulting in overly optimistic CLmax levels. This would be hard to correct within the SST model and in any case would require expert knowledge in turbulence modeling. Within the GEKO model, separation prediction can easily be adjusted by changing even by a non-expert.

Figure 12.178: Prediction of lift and pressure coefficients with GEKO model for DU-96-W-180 (Left) and DU-97-W-300 (Right) airfoil at [28]

Figure 12.179: Prediction of lift coefficient in wide range of angle of attacks (Left) and pressure coefficient for (Right) with GEKO model for S805 airfoil at [23]

Figure 12.180: Prediction of lift coefficient wide range of angle of attacks (Left) and pressure coefficient for (Right) with GEKO model for S825 airfoil at [24]

Figure 12.181: Prediction of lift coefficient in wide range of angle of attacks (Left) and pressure coefficient for (Right) with GEKO model for S809 airfoil at [25]

Figure 12.182: Prediction of lift coefficient in wide range of angle of attacks (Left) and pressure coefficient for (Right) with GEKO model for S814 airfoil at [26]

It is important to understand that changes of affect not only boundary layers, but the entire flow field. Increasing reduces the eddy-viscosity in all parts of the domain, including for free shear flows (e.g. mixing layers etc.). Frequently, the adjustment of boundary layer separation is the main optimization requirement and it is desirable to maintain the performance and calibration for free shear flows (e.g. spreading rates for mixing layers and jets etc.). In order to avoid any negative impact of on free shear flows, the reduction in eddy-viscosity is corrected by modifying accordingly. This is achieved through the correlation given in Equation (2.11). This correlation increases with increasing to maintain the spreading rates for mixing layers. As the correlation =CMixCor is default, users do not have to adjust when changing . This effect will be demonstrated in the Section 3.3 dealing with the impact of .

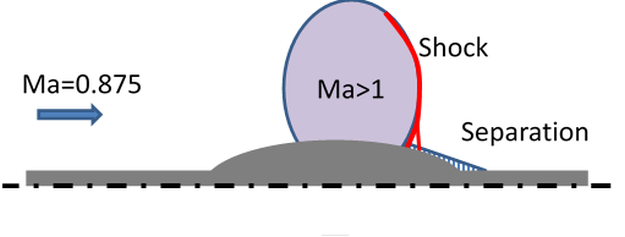
The Bachalo-Johnson NASA Bump flow experiment [2], as depicted in Figure 12.183: Schematic of transonic axi-symmetric bump flow, features a subsonic inflow with Ma=0.875. The flow is then accelerated to supersonic speed over the bump and then reverts to subsonic speed through a shock wave. The shock causes the boundary layer behind the shock to separate, which in turn interacts with the shock by pushing it forward. The ability to predict the shock location is therefore directly linked to a model's ability to predict boundary layer separation. As expected, again, the models group as GEKO-1.75/SST and GEKO-1.00/RKE as seen from Figure 12.184: Pressure coefficient,, along wall of bump. Comparison of different GEKO settings with RKE and SST model and experimental data [2].. Both, the GEKO-1.75 and the SST model can predict the shock location and the post-shock separation zone properly. The GEKO-1.00/RKE models fail due to their lack of separation sensitivity.

Figure 12.183: Schematic of transonic axi-symmetric bump flow

Figure 12.184: Pressure coefficient,, along wall of bump. Comparison of different GEKO settings with RKE and SST model and experimental data [2].

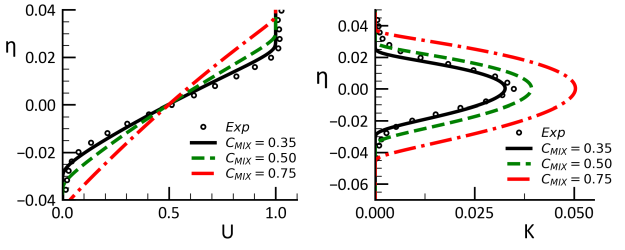
The coefficient is introduced to allow a modification of the model characteristics in the near wall region under non-equilibrium conditions. It has a strong effect on heat transfer predictions in reattachment and stagnation regions.

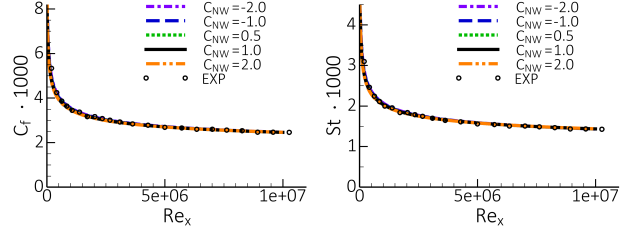
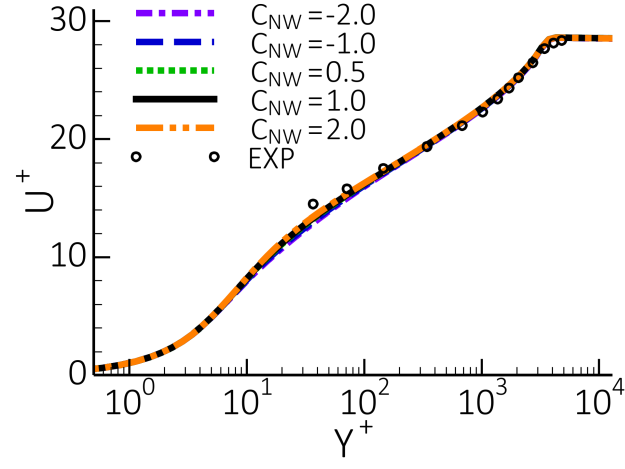
The first task is to show that variations in (like ) do not affect flat plate boundary layer behavior. This can be seen from Figure 12.185: Flat plate boundary layer under variation of (=1.75). Left: Wall-shear stress coefficient, , Right: Wall heat transfer coefficient, St. where both, the wall shear stress coefficient,, and the wall heat transfer coefficient St are unaffected by variations in . In addition, the velocity profile in log-scale is maintained as shown in Figure 12.186: Velocity profiles in logarithmic coordinates - variation of (=1.75). Many more variations of parameters and have been tested and the agreement is like that shown in Figure 12.186: Velocity profiles in logarithmic coordinates - variation of (=1.75).

Figure 12.185: Flat plate boundary layer under variation of (=1.75). Left: Wall-shear stress coefficient, , Right: Wall heat transfer coefficient, St.

Figure 12.186: Velocity profiles in logarithmic coordinates - variation of (=1.75)

The effect of changing for the axisymmetric diffuser test case CS0 [10] is shown in Figure 12.187: Impact of variation in on CS0 diffuser flow [10]. Left: Wall shear-stress coefficient, . Right: Wall pressure coefficient (=1.0, =0.0, =0.9). The coefficient is designed to have an influence mostly near the wall. Therefore, the wall shear-stress distribution shows a much larger sensitivity to this variation (Figure 12.187: Impact of variation in on CS0 diffuser flow [10]. Left: Wall shear-stress coefficient, . Right: Wall pressure coefficient (=1.0, =0.0, =0.9) Left) than the Cp-distribution (Figure 12.187: Impact of variation in on CS0 diffuser flow [10]. Left: Wall shear-stress coefficient, . Right: Wall pressure coefficient (=1.0, =0.0, =0.9) Right). The velocity profiles shown in Figure 12.188: Impact of variation in on velocity profiles for CS0 diffuser flow [10] illustrate the effect more clearly. Contrary to changes of , where the entire boundary layer is affected, variations in change only the inner part of the velocity profiles.

Figure 12.187: Impact of variation in on CS0 diffuser flow [10]. Left: Wall shear-stress coefficient, . Right: Wall pressure coefficient (=1.0, =0.0, =0.9)

Figure 12.188: Impact of variation in on velocity profiles for CS0 diffuser flow [10]

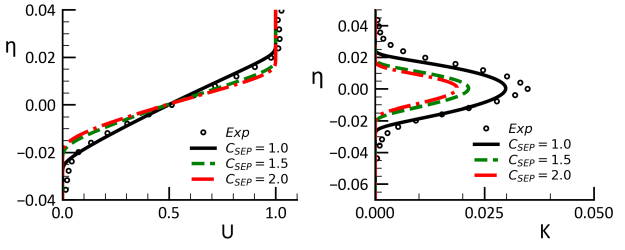
For non-equilibrium flows, the wall shear stress and more importantly, the heat transfer to a wall, depend mostly on the model details close to the wall. The coefficient can be tuned to allow fine-tuning for such flows. An example is backward-facing step with Cf and heat transfer measurements, St, downstream of the step [31]. The effect is shown in Figure 12.189: Backward-facing step with heat transfer under variation of (Top:=1.00, Bottom: =1.75, Both: =0.9, =). Left: Wall shear stress coefficient, , Right: Heat transfer Stanton number. It is computed with both, =1.0 and =1.75, =CMixCor , =0.9 and a variation in . The heat transfer is strongly affected (and can therefore be optimized) by changes in . In the current application, the optimal value is =0.5 for both values of . =0.5 is also the default setting. It is important to note that is a minor parameter and will likely not have to be tuned for most flows. Wider validation studies indicate that the default value is suitable for most applications.

Figure 12.189: Backward-facing step with heat transfer under variation of (Top:=1.00, Bottom: =1.75, Both: =0.9, =). Left: Wall shear stress coefficient, , Right: Heat transfer Stanton number

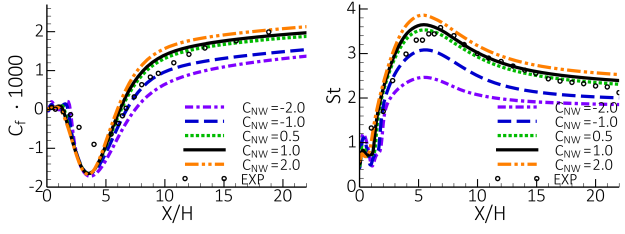
The parameter affects only free shear flows. It has no impact on boundary layers due to the blending function FBlend. Increasing leads to larger eddy-viscosity (higher turbulence levels) in free shear flows. This is illustrated in Figure 12.190: Impact of variation in on mixing layer when using the =2(=0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles which shows results for a mixing layer simulation compared with experimental data [3]. As expected, increasing leads to larger spreading rates of the velocity profile, associated with higher levels of turbulence kinetic energy. In most applications, it is desirable to calibrate the coefficient such that a good agreement with mixing layer flows is achieved (in the current example with =2 this means =0.35). However, there can be cases, where stronger mixing is desired and where the calibration for a classical mixing layer is not sufficient. Examples are flows with strong mixing characteristics, like flows past bluff bodies etc. It should be emphasized that the physical reason for increased mixing in such cases is often a result of flow unsteadiness (e.g. vortex shedding) augmenting the conventional turbulence mixing. In such cases it will not be possible to obtain a perfect agreement against data, as such unsteady effects are typically stronger than that which a turbulence model can provide. Still, increasing can at least compensate for some of the missing effects, in case that unsteady (scale resolving) simulations are not feasible.

Figure 12.190: Impact of variation in on mixing layer when using the =2(=0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles

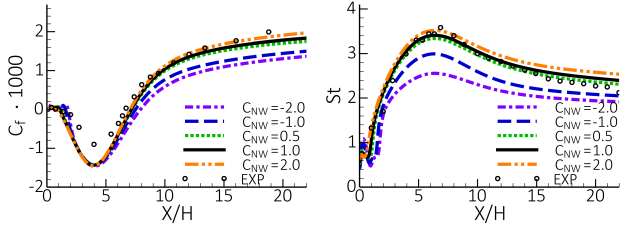
As already mentioned in the section on (section 3.1), there is a subtle interaction of and which users have to understand. Variations in also affect free shear flows and increases in result in lower spreading rates. This can be seen in Figure 12.191: Impact of variation in on mixing layer (=0, =0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles which shows the results of a variation for the mixing layer [3] ( = 0, = 0.9, = 0.5). Here the solution with = 1 is closest to the data whereas the solution with =2 predicts far too low spreading rates and turbulence levels. The effect on the eddy-viscosity is even stronger than for the boundary layer resulting in a reduction of more than a factor 3 with increasing (not shown).

Figure 12.191: Impact of variation in on mixing layer (=0, =0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles

In order to compensate the effect of on free shear flows, the coefficient has to be increased with increasing . This is achieved by the correlation CMixCor given in Equation (2.11) which is the model default. The correlation is provided so that users know which value is optimal for a given setting. Increasing above this value will lead to higher and decreasing it to lower turbulence levels and spreading rates for free shear flows.

The results for mixing layer simulations with = CMixCor are shown in Figure 12.192: Impact of variation in on mixing layer when using the = correlation (=0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles. For all selected values of , the mixing layer is maintained, and correct spreading rates are achieved.

Figure 12.192: Impact of variation in on mixing layer when using the = correlation (=0.9, =0.5). Left: Velocity profile. Right: Turbulence kinetic energy profiles

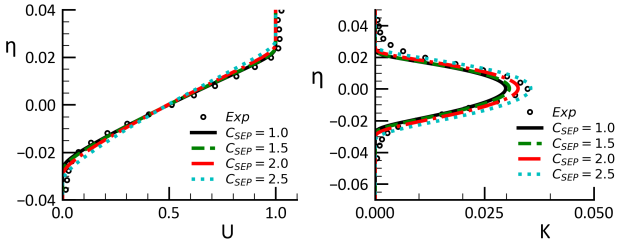
The impact of the parameter is subtle and in most applications it can be maintained at its default value. It is important in cases where jet flows need to be computed with high accuracy. Remember that conventional models like or SST will over-predict spreading rates of round jets substantially while giving reasonable results for plane jets. For this so-called round-jet plane-jet 'anomaly' see e.g. [19,33].

The GEKO model is designed to provide parameter settings which allow an accurate representation of jet flow. This is achieved through the parameter . The way this is achieved is by reducing the influence of (which increases mixing layer spreading rates) on jet flows (especially round jets). It should also be noted that the coefficient is a sub-function of the coefficient . In case =0, the coefficient has no impact.

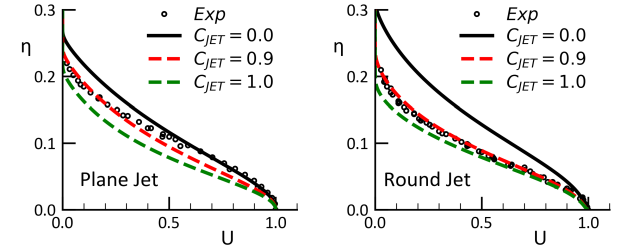
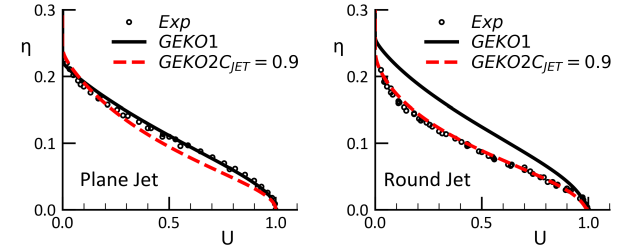
Simulations are again based on self-similar jet-flow equations as given by Wilcox [33]. The two test cases are Wygnanski and Fielder [36] for the plane jet and Bradbury [4] for the round jet. Figure 12.193: Effect of for plane (left) and round (right) jet flow (=2.0, =0.35, =0.5) shows simulations with =2, =0.35 (Correlation) and =0.5 (default). It is clearly seen that the model overpredicts the spreading rates especially for the round jet with =0. The effect of is to reduce the spreading rate of both jet flows, with =0.9 being close to both experimental data-sets. With =2 and =0.9, the model avoids the round jet/plane jet anomaly and predicts lower spreading rates for the round than for the plane jet. Note again, that the changes of discussed here do not affect the mixing layer.

In contrast, Figure 12.194: Comparison of GEKO-1 and GEKO-2 model (with variation of =0.9) shows a comparison between GEKO-1 (=1.0) and GEKO-2 (=1.0) with =0.9. As GEKO-1 is a close cousin of the standard model it behaves just like that model. It gives a correct spreading rate for the plane jet but overpredicts the round jet. Note again, that changes to in GEKO-1 would have no effect, as for that model =0 (so that the sub-model is de-activated).

Figure 12.193: Effect of for plane (left) and round (right) jet flow (=2.0, =0.35, =0.5)

Figure 12.194: Comparison of GEKO-1 and GEKO-2 model (with variation of =0.9)

In summary, in order to achieve optimal performance for round jets, one needs to set to values ~1.75-2.00 and =0.9 (default). With reduction in and the corresponding reduction in , the effect of vanishes.

There is another parameter CJET_AUX which also has an influence on the jet flow. It defines the limit between mixing layers and jet flows. The larger the value, the sharper the 'demarcation' and stronger the effect of . The default value is CJET_AUX =2.0. It is suitable for jet flow simulations to set the value to CJET_AUX =4.0. This is not done by default, as it can lead to oscillations on poor meshes.

Users who do not have a need for accurate predictions of jets can use the default settings for .

It is well known that for rectangular turbulent channel flows, secondary flows develop in the plane normal to the mean flow. Such secondary flow is not present in laminar flows and can also not be represented at all by eddy-viscosity models. The situation is depicted in Figure 12.195: Comparison of streamline velocity contours and secondary motion predicted by linear (Left) and non-linear (Center) GEKO-1.00 model with the DNS (Right) data in the fully developed square duct flow [19] for a square channel. The main flow direction is normal to the plotting plane. The velocity contour colors on the left picture show the main flow as computed by a linear eddy-viscosity model. There are no streamlines when projected into this plane.

The practical effect of this effect is that the secondary flow transports flow (and thereby momentum) into the corner. If the corner flow experiences an adverse pressure gradient, this additional momentum can help the flow to avoid/delay separation. When computing such flows with an eddy-viscosity model, such separations can occur earlier than in the experiments, which in turn can have a substantial effect on the overall performance. The right picture shows the results from a Direct Numerical Simulation (DNS, e.g. [19]) of this flow. There are clearly recognizable secondary streamlines pushing flow into the corners. The center picture shows the GEKO model in combination with an existing non-linear algebraic stress-strain model (Wallin-Johansson Explicit Reynolds Stress Models WJ-EARSM), which can mimic the effect. The WJ-EARSM is fairly complex and the GEKO model was used as a reference point for calibration of the much simpler quadratic stress-strain relationship which can also account for this effect (Equation (2.7)). This term has a free parameter, CCORNER, which can be tuned by the users.

Figure 12.195: Comparison of streamline velocity contours and secondary motion predicted by linear (Left) and non-linear (Center) GEKO-1.00 model with the DNS (Right) data in the fully developed square duct flow [19]

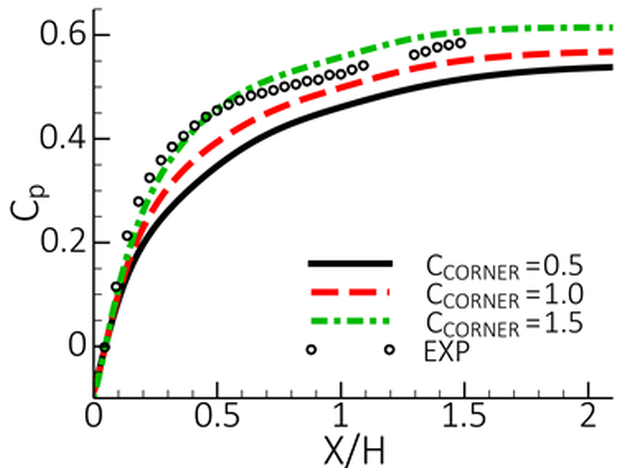
Figure 12.196: Comparison of turbulence models for flow in square channel. Left: GEKO with WJ-EARSM. Middle, GEKO with CCORER=0.9. Right GEKO linear (CCORNER=0.0). shows a comparison for the rectangular channel for GEKO-175 (=1.75 all else default). The left picture shows the combination of GEKO with the WJ-EARSM, the middle picture the combination with the quadratic term and CCORNER=0.9 and the left for CCORNER=0.0. The simple quadratic model gives a good approximation of the flow, similar to the WJ-EARSM.

Figure 12.196: Comparison of turbulence models for flow in square channel. Left: GEKO with WJ-EARSM. Middle, GEKO with CCORER=0.9. Right GEKO linear (CCORNER=0.0).

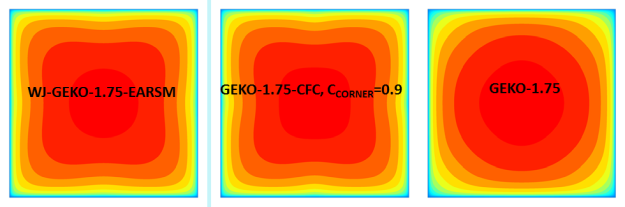
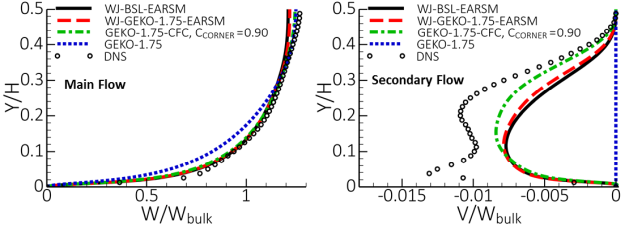
Figure 12.197: Velocity profiles plotted along diagonal of channel for different turbulence models against DNS data. Right: Main flow, Left Secondary Flow shows a comparison of velocity profiles for different turbulence models for the square channel. The right part of the picture shows the secondary flow into the corner along a diagonal of the channel cross-section. Most obviously, the linear model (GEKO-1.75) gives zero velocity along the diagonal. The other models provide fairly similar strength and distributions of the same order as the reference DNS data, but clearly also not in perfect agreement, especially very close to the wall. Note that further increases in for this flow would break the symmetry of the crossflow pattern. The left part of the figure shows the mean flow profile also along the diagonal. The most important effect is the higher velocity close to the wall ('fuller profile') which allows the flow to overcome a stronger pressure gradient before separating.

Figure 12.197: Velocity profiles plotted along diagonal of channel for different turbulence models against DNS data. Right: Main flow, Left Secondary Flow

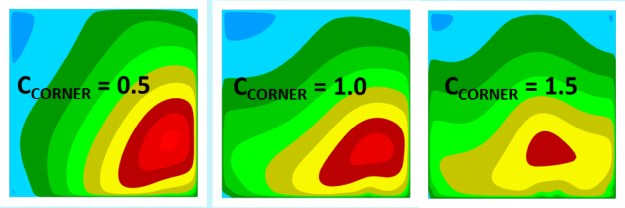
A more challenging example is the flow in a 3D diffuser [5] shown in Figure 12.198: Geometry of 3D diffuser flow [4]. The diffuser has two opening angles, a large one on the upper wall and a small one at the side walls. In the experiments, the flow separates from one of the corners and then attaches to the lower wall. In the simulations, the flow topology depends strongly on the model and the corner flow representation.

Figure 12.198: Geometry of 3D diffuser flow [4]

Figure 12.199: Flow topology for 3D diffuser flow shown through streamwise velocity contour at downstream end of diffuser opening section for GEKO-1.00 with different values. shows the mean velocity contours at the end of the expansion section of the diffuser. Clearly the flow topology depends strongly on the selected values of the corner flow correction term.

The influence of the model changes on the pressure coefficient, Cp, can be seen in Figure 12.200: Wall pressure coefficient,, for 3D diffuser for GEKO-1.00 with different values.. Note that the current flow is very sensitive and hard to compute, but it does demonstrate the importance of corner flow separation for technical flows.

Figure 12.199: Flow topology for 3D diffuser flow shown through streamwise velocity contour at downstream end of diffuser opening section for GEKO-1.00 with different values.

Figure 12.200: Wall pressure coefficient,, for 3D diffuser for GEKO-1.00 with different values.

The curvature correction (CC) is an already existing model, which is accessible to all eddy-viscosity models in Fluent. The only change when integrating it with GEKO was that the coefficient CCURV is now also accessible through a User Defined Function (UDF) and can thus be optimized zonally, or even locally.

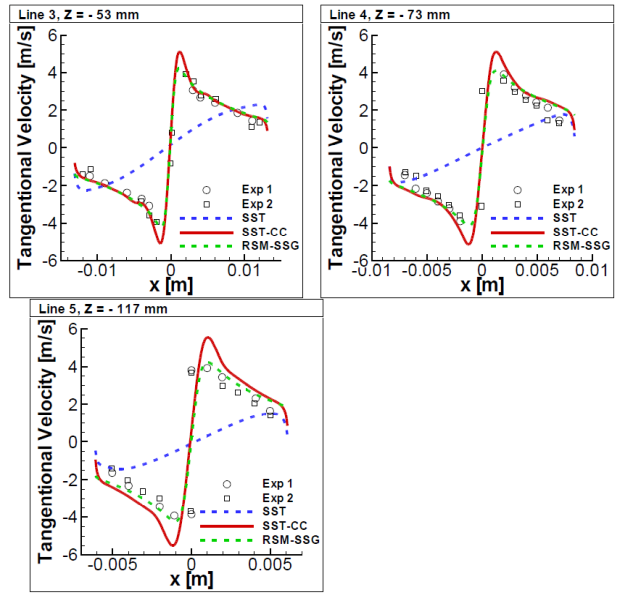
No detailed description of the CC formulation is given, as it is described elsewhere [22]. The effect of the CC can be shown for a hydro-cyclone (see Figure 12.201: Hydrocyclone typical flow structure. Reproduced from Cullivan et al [9].) The flow (typically with particles) enters the domain tangentially through the feed. A strong swirl is generated pushing the particles to the wall and out through the underflow, whereas the cleaned fluid leaves the domain through the overflow. The effect of swirl and rotation cannot be handled by eddy-viscosity models without corrections. The current CC serves this purpose, as can be seen by a comparison of the circumferential velocity profiles for the SST model, the SST-CC and a full Reynolds Stress model (RSM-SSG) in Figure 12.202: Time-averaged profiles of the tangential velocity in the hydrocyclone. Comparison with the experiments of Hartley [13].. While the model without CC produces mostly a solid-body rotation, the SST-CC model gives results much closer to the experiments and similar to a full Reynolds Stress model (note that at the time of writing, the GEKO model has not been run for this test case. However, the effect of the CC is mostly independent of the underlying model formulation).

Figure 12.201: Hydrocyclone typical flow structure. Reproduced from Cullivan et al [9].

Figure 12.202: Time-averaged profiles of the tangential velocity in the hydrocyclone. Comparison with the experiments of Hartley [13].

The blending function activates the coefficients /. In order to avoid any impact on boundary layers, the blending function is designed such that these parameters have only a minor effect there. In most cases the users will not have to change the function FGEKO (in Fluent it is called 'Blending Function for GEKO'). However, there are several ways to modify the function in case it is needed.

The easiest way is to adjust the coefficients exposed in the GUI. For fully turbulent flows (no transition model) there is only one coefficient called CBF_TURB (GEKO). Increasing it will increase the thickness of the near wall 'shielding' and decreasing it will decrease the 'shielding' from / inside the boundary layer. This effect can be seen in Figure 12.203: Effect of CBF_TURB on for flow around airfoil. Left CBF_TURB=2.0. Right: CBF_TURB=4.0. for the flow around a NACA 4412 airfoil. The lefts side of the figure shows the default setting (CBF_TURB=2) and the right side the function for CBF_TURB=4. The thickness of the boundary layer 'shielding' is clearly increased on the right part of the figure.

There is a second coefficient for this function, which is a bit more involved. It is introduced to allow protection of the laminar boundary layer from the / term. This is desirable in case of transition predictions [16], where otherwise the / term can affect the transition location. For this purpose, a second coefficient, CBF_LAM (GEKO) is used in case a transition model is selected. The effect is shown in Figure 12.204: Effect of CBF_LAM on for flow around airfoil. Left CBF_LAM=1.0 (default for turbulent simulations). Right: CBF_LAM=25 (default for transitional simulations). . The left figure shows the turbulent default (CBF_TURB=2.0, CBF_LAM=1.0 same as Figure 12.203: Effect of CBF_TURB on for flow around airfoil. Left CBF_TURB=2.0. Right: CBF_TURB=4.0. Left) and the right part shows the increase to its default for transitional simulations (CBF_TURB=2.0 CBF_LAM=25.0). As can be seen from the right part of Figure 12.203: Effect of CBF_TURB on for flow around airfoil. Left CBF_TURB=2.0. Right: CBF_TURB=4.0., the coefficient CBF_LAM provides increased shielding, especially in the leading edge region. In case of fully turbulent settings (no transition model), users can only access CBF_TURB (CBF_LAM=1.0 is fixed by default). The parameter CBF_LAM becomes available once a transition model is selected. The coefficient CBF_LAM needs to always satisfy .

Figure 12.203: Effect of CBF_TURB on for flow around airfoil. Left CBF_TURB=2.0. Right: CBF_TURB=4.0.

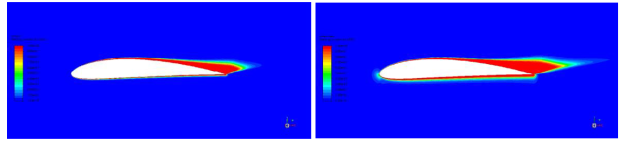
Figure 12.204: Effect of CBF_LAM on for flow around airfoil. Left CBF_LAM=1.0 (default for turbulent simulations). Right: CBF_LAM=25 (default for transitional simulations).

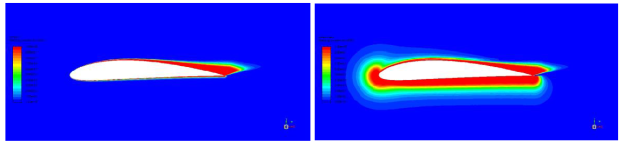
Finally, the function FGEKO can be adjusted through a User Defined Function (UDF). Users can either over-write the function in the entire domain, or only in certain parts, as the original function is accessible in the UDF. This could make sense in areas where free shear flows and boundary layers cannot be easily discerned by the function itself, especially when is increased to obtain more mixing in the free shear flow region.

An example of such a flow is shown in Figure 12.205: Blending function for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF for a multi-element airfoil. Assume, the wake of the slat (upstream airfoil) over the main airfoil is of interest. Assume that the default settings provide not enough mixing in this region, hence an increased mixing through increases in is desired. This works for moderate increases in , but large increases (like =3) lead to decreasing efficiency of the term. The reason is that through increases in the eddy-viscosity, the blending function becomes activated also in the wake, due to the proximity of the main airfoil wall. This is shown in the upper right of Figure 12.205: Blending function for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF, where one can clearly see the activation of the blending function in the wake of the slat. To counter such an effect, one can over-write the blending function. In the current case, a function based on wall-distance was used as shown in the bottom left of Figure 12.205: Blending function for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF. Note that this is just a generic example to demonstrate the issues and no effort was made to optimize the bending function. The effect of the change in the function is seen in Figure 12.206: Ratio of turbulence to molecular viscosity for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF which shows the ratio of turbulence to molecular viscosity for the blending functions and settings shown in Figure 12.205: Blending function for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF. Clearly, the ratio increase from the left (default settings) to the middle picture. However, the increase is moderate. When restricting the function FGEKO to the immediate boundary layer around the main wing, the effect of increasing becomes much stronger, resulting in a substantial increase in the viscosity ratio (Figure 12.206: Ratio of turbulence to molecular viscosity for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF – right).

It needs to be stressed again, that such modifications of are typically not required and the flexibility of provided by simply changing coefficients is sufficient in most cases. However, the discussion shows the versatility of the current GEKO models implementation.

Figure 12.205: Blending function for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF

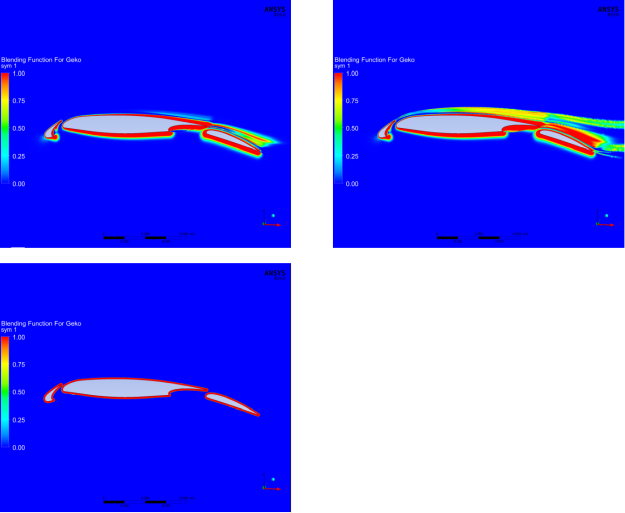
Figure 12.206: Ratio of turbulence to molecular viscosity for multi-element airfoil. Upper left: Default =1.75, ==0.303. Upper right: =3. Bottom left: through UDF

A more dramatic example of how the change in blending function can affect results is given by the flow around a triangular cylinder. The set-up is shown in Figure 12.207: Flow around triangular cylinder [37].

Figure 12.207: Flow around triangular cylinder [37]

The cylinder has an edge length of , the height of the channel is . The inlet velocity is . The simulation is carried out in steady state mode – and converges to a steady state solution (which is not always possible with bluff body flows). The real flow is of course unsteady with strong vortex shedding in addition to turbulence created unsteadiness. The vector field depicted shows a very large separation zone downstream of the cylinder, as expected. The simulation was carried out with GEKO-1.75 (default) under steady-state conditions.

In order to test by how much, the re-circulation zone can be reduced, the coefficient was increased. The results are shown in Figure 12.208: GEKO-1.75 solution under variation of . Left: Velocity U. Middle: Eddy-viscosity ratio. Right: using built-in function [28] when using the built-in version of the function. The recirculation (line in middle figure) decreases with increasing . However, eventually, the entire separation zone lies within the =1 region and no further effect can be achieved by increasing .

Figure 12.208: GEKO-1.75 solution under variation of . Left: Velocity U. Middle: Eddy-viscosity ratio. Right: using built-in function [28]

The same tests are shown in Figure 12.209: GEKO-1.75 solution under variation of . Left: Velocity U Middle: Eddy-viscosity ratio. Right: using UDF-based function [28] but with the help of a UDF-based function. As shown in the right part of the figure, is defined only within a given wall distance as =1 and is switched to free shear flow status outside. This avoids the restriction of the impact of increasing and allows a further reduction in the re-circulation zone due to increased mixing.

Figure 12.209: GEKO-1.75 solution under variation of . Left: Velocity U Middle: Eddy-viscosity ratio. Right: using UDF-based function [28]

The comparison with experimental data along the center-line downstream of the cylinder is shown for both variants in Figure 12.210: Center line velocity for triangular cylinder. Left: GEKO-1.75 with built-in function. Right: GEKO-1.75 with UDF-based function [28]. The left part of the figure shows the solution using the built-in function for and the right part shows the solution using a wall-distance-based UDF variant (as shown in right part of Figure 12.209: GEKO-1.75 solution under variation of . Left: Velocity U Middle: Eddy-viscosity ratio. Right: using UDF-based function [28]). Clearly, the UDF based variant allows a much stronger reduction in separation size. It should be noted that none of the simulations is able to produce the fairly strong backflow velocity in the re-circulation zone. This should not come as a surprise, as it is mostly a result of very strong backflow events in the unsteady vortex shedding cycle of the experiment, which cannot be captured by a steady state solution. Nevertheless, it is important to observe the much better agreement in flow recovery downstream of the recirculation zone. In case of more complex arrangements, any additional parts of the geometry downstream of the triangular cylinder would see a much more realistic approaching flow field than with the default settings.

Figure 12.210: Center line velocity for triangular cylinder. Left: GEKO-1.75 with built-in function. Right: GEKO-1.75 with UDF-based function [28]

The realizability coefficient is set to its standard value of =0.577. The value should typically not be changed but is accessible for special situations. However, it was found that limiters can have a strong effect for flows which are severely under-resolved. An example would be an inlet condition for the velocity field, where the velocity in the lower half of the inlet has one value and in the upper half another. At the jump between these two values, the flow is under-resolved and the coefficient could potentially delay the growth of the mixing layer. Note that for such flows, the production limiter could have a similar effect. If this is the case, it would be an option to set both limiters to very large values and instead activate the Kato-Launder limiter.

The coefficient CNW_SUB allows for slight re-tuning of the log-layer shift which will also affect the wall shear stress distribution for boundary layers. Increasing its value from CNW_SUB=1.7 will shift the log-layer more into the laminar direction (up) and decrease the wall shear stress.