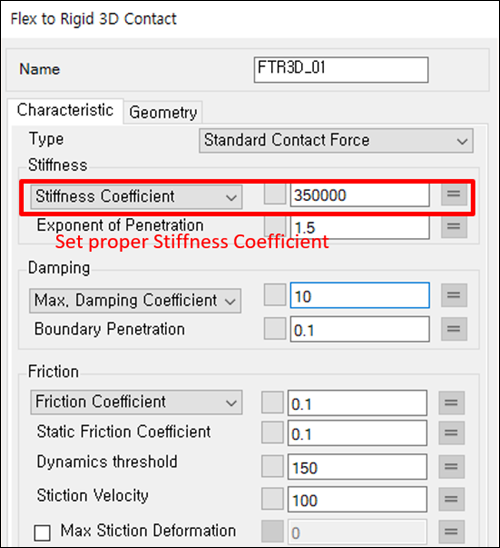
The Exponent of Penetration parameter represents the non-linear characteristic of force versus displacement. The default value is highly recommended for the most problems, but you should adjust the value if your solution does not properly represent the physical phenomenon.
For Rigid body contact, penetration refers to the local deformation that occurs in the contact area and stiffness refers to the elasticity. For FE contact, penetration does not make sense physically but the Stiffness Coefficient (K) must still be defined.
A low value of K makes for good numerical convergence but allows large penetration. A high K value reduces penetration, but it causes numerical instability because a small variation of penetration causes a big variation in force. You should therefore use a lower value within the allowable penetration range.
A relatively large Exponent of Penetration (1.5 to 2) also helps to reduce sensitivity to forces at the beginning of contact.
In order to achieve an accurate solution, K and n values for the contact must also be determined depending on the geometry shape and material.
The Stiffness Coefficient can be calculated from the equation shown below:
(16–5) |
where,
= contact stiffness coefficient
= Normal direction force acting on contact
= allowable contact penetration
= exponent of penetration
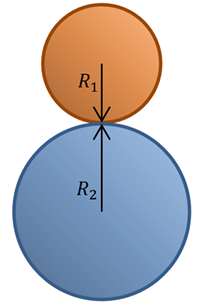
When dealing with Hertzian contact between 2 spheres, the contact stiffness coefficient should be calculated by:
(16–6) |
This is derived from the Hertzian contact theory:
(16–7) |
where,
(16–8) |
(16–9) |
and,
,
,
and
= Young's modulus and Poisson's ratio of each sphere
and
= radius of each sphere