Thermal Analysis can be used to calculate the temperature, thermal strain and stress of a body under heat conduction and convection. Nodal flexible and nodal EasyFlex bodies are available in this analysis. The governing equations for the steady state thermal analysis can be represented by the following equation.
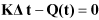 | (9–19) |
where 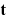 and
and 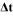 are the nodal temperature vector and its
change in the NR iteration.
are the nodal temperature vector and its
change in the NR iteration. 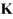 is
the thermal conductivity matrix of the body.
is
the thermal conductivity matrix of the body. 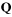 is the nodal heat flow vector such as heat
flow input, convection, and internal heat generation. In general, the thermal
conductivity matrix can be calculated using the following equation.
is the nodal heat flow vector such as heat
flow input, convection, and internal heat generation. In general, the thermal
conductivity matrix can be calculated using the following equation.
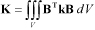 | (9–20) |
Where 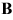 and
and 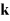 are the partial derivative of the shape
function and the conductivity matrix which is defined from the material properties.
The nodal thermal strain can be calculated by using the following equation.
are the partial derivative of the shape
function and the conductivity matrix which is defined from the material properties.
The nodal thermal strain can be calculated by using the following equation.
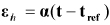 | (9–21) |
where 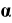 and
and 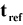 are the thermal expansion coefficient and the
reference temperature which is defined from the material properties.
are the thermal expansion coefficient and the
reference temperature which is defined from the material properties.
In transient thermal analysis, the heat capacity effect is required in the steady-state thermal analysis. The governing equations for the transient thermal analysis can be represented as follows.
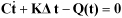 | (9–22) |
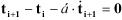 | (9–23) |
Where 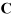 and
and 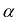 are the heat capacity matrix and the
coefficients of the integrator. The heat capacity matrix can be calculated using the
following equation.
are the heat capacity matrix and the
coefficients of the integrator. The heat capacity matrix can be calculated using the
following equation.
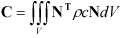 | (9–24) |
Where 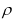 and
and 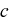 are the density and specific heat which is
defined from the material properties.
are the density and specific heat which is
defined from the material properties. 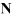 is the shape function.
is the shape function.


