Initial analysis can be used to understand the arrangement of bodies from the relative position and angle due to motion or the initial conditions of joints, and to calculate the initial velocity of a body by considering its kinematic relationship with other bodies. Forces and the acceleration of the body are calculated during this analysis. This analysis would also be run at the initial time when system analysis such as Static, Dynamic and Eigenvalue analysis is carried out. Initial analysis has three types, namely position, velocity and acceleration analysis.
Position analysis solves the positions and orientations of bodies while minimizing constraint violation at the position level. The governing equations for position analysis can be represented as in the following equations.
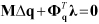 | (9–1) |
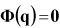 | (9–2) |
where 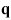 and
and 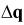 are the generalized coordinates to represent
the position and orientation of the body and its change in the NR (Newton Raphson)
iteration.
are the generalized coordinates to represent
the position and orientation of the body and its change in the NR (Newton Raphson)
iteration. 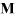 and
and 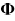 are the mass matrix of the body and the
constraint equation, respectively.
are the mass matrix of the body and the
constraint equation, respectively. 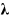 is the Lagrange multiplier, which is
introduced as the classical method in mechanics. In this step, flexible EasyFlex and
modal flexible bodies are assumed to be rigid bodies.
is the Lagrange multiplier, which is
introduced as the classical method in mechanics. In this step, flexible EasyFlex and
modal flexible bodies are assumed to be rigid bodies.
Velocity analysis determines the velocities of bodies with small or redundant initial velocities while minimizing constraint violation at the velocity level. The governing equations for velocity analysis can be represented by the following equations.
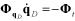 | (9–3) |
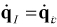 | (9–4) |
where 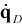 ,
, 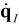 and
and 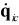 are the dependent coordinate, independent
coordinate and user-defined initial velocity of the body. The information of
dependent and independent coordinates is written in the message file which is
decribed in the Solver Message Manual.
are the dependent coordinate, independent
coordinate and user-defined initial velocity of the body. The information of
dependent and independent coordinates is written in the message file which is
decribed in the Solver Message Manual. 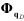 and
and 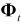 are the partial derivatives of the constraint
equation for the dependent coordinate and time, respectively. If the given initial
velocity of a body is not applied in the system, the body will not have an
independent coordinate. If you change the body on which the initial velocity is
applied to another body with an independent coordinate, the initial velocity will be
reflected in this analysis. In this step, flexible EasyFlex and modal flexible
bodies are assumed to be rigid bodies.
are the partial derivatives of the constraint
equation for the dependent coordinate and time, respectively. If the given initial
velocity of a body is not applied in the system, the body will not have an
independent coordinate. If you change the body on which the initial velocity is
applied to another body with an independent coordinate, the initial velocity will be
reflected in this analysis. In this step, flexible EasyFlex and modal flexible
bodies are assumed to be rigid bodies.
Acceleration analysis determines forces and the acceleration of bodies while satisfying the constraint equation and equation of motion to zero. The governing equations for acceleration analysis can be represented by the following equations.
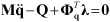 | (9–5) |
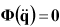 | (9–6) |
where 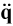 ,
, 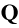 and
and 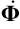 are the generalized acceleration to represent
the acceleration of the body, the force such as contact, internal finite element
force and the constraint equation at the acceleration level. In this step, the
variables for flexible and EasyFlex bodies and system equations such as variable
equations and differential equations are solved simultaneously.
are the generalized acceleration to represent
the acceleration of the body, the force such as contact, internal finite element
force and the constraint equation at the acceleration level. In this step, the
variables for flexible and EasyFlex bodies and system equations such as variable
equations and differential equations are solved simultaneously.


