Next in the workflow is the definition of the fluid transport models using the Transport workflow tree item. The Editor panels for the two items under the Transport node, Fluid Properties and Turbulence, are described below.
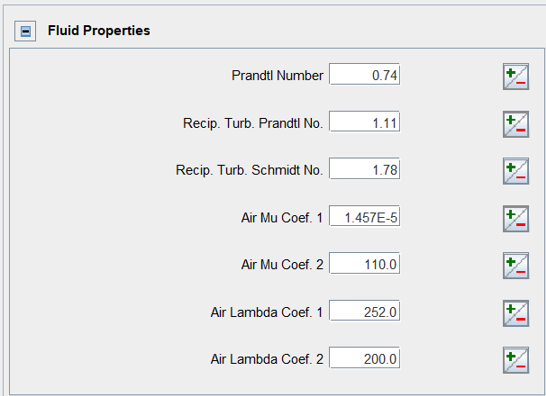
The Transport Editor panel provides settings for Fluid Properties. The input parameters on this panel are used to calculate the fluid properties affecting molecular and turbulent transport processes. Figure 3.14: Input parameters related to the Fluid Properties lists these parameters and their default values. Their definitions and usage are explained in the following paragraphs and also described in the tool tips.
Prandtl Number: Prandtl number of the laminar fluid flow, defined as
(3–2)
where
is the specific heat at constant pressure,
is dynamic viscosity of laminar flow, and
is thermal conductivity of laminar flow. Note that
is only used in the wall heat transfer model.
Recip. Turb. Prandtl Number and Recip. Turb Schmidt Number: The reciprocals of turbulent Prandtl Number and turbulent Schmidt Number. These two parameters are used to convert dynamic viscosity into thermal diffusivity and mass diffusivity, respectively, for turbulent flow transport calculation. The turbulent Prandtl Number and turbulent Schmidt Number are defined as:
(3–3)
(3–4)
Where
is turbulent thermal diffusivity,
is turbulent mass diffusivity,
is turbulent kinematic viscosity. The effective dynamic viscosity for turbulent flows,
, is described in Calculation of Dynamic Viscosity.
Air Mu Coef. 1 (
) and Air Mu Coef. 2 (
): Coefficients in the Sutherland's formula for calculating laminar viscosity of the gas as a function of temperature:
(3–5)
More information about the laminar viscosity calculation is in Calculation of Dynamic Viscosity.
Air Lambda Coef. 1 (
) and Air Lambda Coef. 2 (
): Coefficients in the correlation for calculating laminar thermal conductivity of the flow as a function of temperature:
(3–6)
Note that
is only used in spray vaporization model for computing the thermal conductivity of air. For thermal diffusivity in general, refer to Calculation of Thermal Diffusivity.
Note: Ansys recommends accepting the defaults under Fluid Properties for most engine cases.
In addition to the Fluid Properties, you may also specify Body Acceleration on the Transport Editor panel. The Body Acceleration in X, Y, and Z Direction can be used to specify acceleration due to gravity.
Transport Total Energy: For high-speed flow simulations, it may be desirable to transport the total energy of the fluid instead of transporting the internal energy alone in the energy transport equation formulation. The total energy includes both internal energy and kinetic energy. By default, only internal energy is transported in the energy conservation equation. Such a treatment is appropriate for low-speed flows because the kinetic energy is small compared to the internal energy. For high-speed flows, such as supersonic flows, the kinetic energy may no longer be negligible, and you can check the Transport Total Energy box to transport total energy in the energy equation.
In the Forte application, the effective dynamic viscosity for turbulent flows,
, is the sum of two terms, a laminar term and a turbulent term. Taking the
RANS turbulence model (Reynolds-Averaged-Navier-Stokes (RANS) Approach in the Ansys Forte Theory Manual) as
an example, the effective dynamic viscosity is
(3–7) |
where and
are turbulent kinetic energy and its dissipation rate, respectively, and
is a constant in the RANS turbulence model. Most applications of Ansys Forte
software consider turbulent flows. In turbulent flow simulations, the laminar viscosity term
is typically much smaller than the turbulent term, and hence the effective
dynamic viscosity is simply noted as
.
We now describe how to calculate the laminar viscosity . For gas-phase simulations that do not use sprays (Equation 3–5), the laminar viscosity
is calculated by Equation 3–5. The gas mixture species do not affect
usage of this equation. In other words, we use this equation regardless of what species are
present in the gas mixture.
For simulations that use sprays (Spray Model),
because there is fuel vapor in the gas mixture, the gas laminar dynamic viscosity
is a binary average of the air viscosity and the fuel vapor viscosity. While
the air viscosity is still calculated by Equation 3–5, the fuel vapor viscosity is a mass average
of each fuel vapor species' viscosity. The species viscosity is calculated by
Equation 10 in Vapor Viscosity.
In Forte software, the effective thermal diffusivity is the turbulent thermal
diffusivity () because it is much larger than the laminar one. It is calculated by
Equation 3–7, using the user input Recip. Turb. Prandtl Number and the turbulent viscosity discussed in
Calculation of Dynamic Viscosity. It is
used to compute a turbulent diffusion term in the energy equation; see
Equation 2–17 in the Ansys Forte Theory Manual.
In Forte, the effective mass diffusivity is the turbulent mass diffusivity
() because it is much larger than the laminar one. It is calculated by Equation 3–4, using the user input
Recip. Turb. Schmidt Number and the turbulent viscosity
discussed in Calculation of Dynamic Viscosity. Turbulent mass diffusivity is used to compute a
turbulent diffusion term in the species transport equation, see
Equation 2–16 in the Ansys Forte Theory Manual.
Use the Turbulence Editor panel to select among choices for the Turbulence Model: RANS (Reynolds-Averaged Navier-Stokes) or LES (Large-Eddy Simulation) models. For the RANS models, options of RNG k-epsilon or k-epsilon are offered. For LES models, the options of Smagorinsky or Dynamic Structure model are available. Select no model for a laminar flow simulation.
For a simulation with the RANS approach, the default choice of RNG (Re-Normalization Group) k-epsilon is recommended, although a standard k-epsilon model may also be selected.
Note: Ansys recommends using the RNG-k-epsilon model for engine cases and for spray-chamber cases. The spray models have many years of calibration to this model and are unlikely to work as well with the k-epsilon model. The RNG-k-epsilon model should also be a better model for engine combustion. The standard model is included for research purposes or for use with problems such as pure air flow, for example, where it might be more appropriate.
For a simulation with the LES approach, the Dynamic Structure model is recommended. The Smagorinsky model is included due to its simplicity and historical importance. However, it is considered as over-dissipative and less accurate compared to the Dynamic Structure model.
For the turbulence model selected, there are a number of model parameters displayed. However, the default values are recommended. Details on how the turbulence equations use these parameters are included in the Ansys Forte Theory Manual.