The Lee model [350] is a mechanistic model with a physical basis. It is used with the mixture and VOF multiphase models and can be selected with the Eulerian multiphase model if one of the overall interfacial heat transfer coefficient models will be used (as opposed to the two-resistance model). In the Lee model, the liquid-vapor mass transfer (evaporation and condensation) is governed by the vapor transport equation:

(14–609)

As shown in the right side of Equation 14–609, Ansys Fluent defines positive mass transfer as being from the liquid to the vapor for evaporation-condensation problems.

Based on the following temperature regimes, the mass transfer can be described as follows:

If (evaporation):

(14–610)

If (condensation):

(14–611)

is a coefficient that must be fine tuned and can be interpreted as a relaxation time. and are the phase volume fraction and density, respectively. The source term for the energy equation can be obtained by multiplying the rate of mass transfer by the latent heat.

Consider the Hertz Knudsen formula [239] [315], which gives the evaporation-condensation flux based on the kinetic theory for a flat interface:

(14–612)

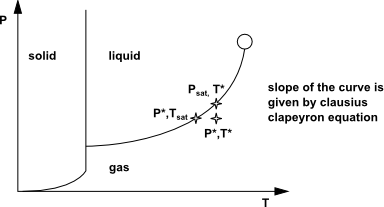
The flux has units of kg/s/m², is the pressure, is the temperature, and is the universal gas constant. The coefficient is the so-called accommodation coefficient that shows the portion of vapor molecules going into the liquid surface and adsorbed by this surface. represents the vapor partial pressure at the interface on the vapor side. The Clapeyron-Clausius equation relates the pressure to the temperature for the saturation condition. (It is obtained by equating the vapor and liquid chemical potentials):

(14–613)

and are the inverse of the density for the vapor and liquid (volume per mass unit), respectively. is the latent heat (J/kg).

Based on this differential expression, we can obtain variation of temperature from variation of pressure close to the saturation condition.

Figure 14.13: The Stability Phase Diagram

The Clausius Clapeyron equation yields the following formula as long as and are close to the saturation condition:

(14–614)

Using this relation in the above Hertz Knudsen equation yields [645]

(14–615)

The factor is defined by means of the accommodation coefficient and the physical characteristics of the vapor. approaches 1.0 at near equilibrium conditions.

In the Eulerian and mixture multiphase models, the flow regime is assumed to be dispersed. If we assume that all vapor bubbles, for example, have the same diameter, then the interfacial area density is given by the following formula:

(14–616)

where is the bubble diameter () and the phase source term (kg/s/m³) should be of the form:

(14–617)

From the above equation, , which is the inverse of the relaxation time (1/s) is defined as

(14–618)

This leads to the final expression for the evaporation process defined in Equation 14–610. It can be treated implicitly as a source term in the phase conservation equation.

A similar expression can be obtained for condensation. In this case, we consider small droplets in a continuous vapor phase even if your primary phase is a liquid.

Note that the coefficient should theoretically be different for the condensation and evaporation expression. Furthermore, the theoretical expression is based on a few strong assumptions:

The bubble diameter and accommodation coefficient are usually not very well known, which is why the coefficient must be fine tuned to match experimental data. By default, the coefficient for both evaporation and condensation is 0.1. However, in practical cases, the order of magnitude of can be as high 10³.

The thermal phase change model is available for evaporation-condensation when the Eulerian multiphase model is used with the two-resistance approach for computing phase heat transfer coefficients (Two-Resistance Model).

Applying Equation 14–390 and Equation 14–391 to a liquid-vapor pair gives:

where and are the liquid and vapor phase heat transfer coefficients, and are the liquid and vapor phase enthalpies, and and are the scaling factors. By default, and are set to 1. The interfacial temperature is determined from consideration of thermodynamic equilibrium. Ignoring effects of surface tension on pressure, we can assume that , the saturation temperature.

Because neither heat nor mass can be stored on the phase interface, the overall heat balance must be satisfied:

(14–621)

From the preceding equations, the mass transfer through evaporation from the liquid to the vapor phase can be expressed as:

(14–622)

The phase enthalpies, and , need to be computed correctly to take account of the discontinuity in static enthalpy due to latent heat between the two phases as well as the heat transfer from either phase to the phase interface. Using the Prakash formulation [532] with the bulk fluid enthalpy carried out of the outgoing phase and the saturation enthalpy carried into the incoming phase we have:

If (evaporation, the liquid phase is the outgoing phase):

(14–623)

If (condensation, the liquid phase is the incoming phase):

(14–624)

This leads to a formulation that is stable both physically and numerically. It implies that the denominator in Equation 14–622 is non-zero, being greater than or equal to the latent heat:

(14–625)

It may be noted that with the presence of mass transfer and are total phase enthalpies, which can be expressed in a general form:

(14–626)

where is the reference temperature and is the standard state enthalpy at . Equation 14–626 applies for phases as well as species on each phase.

Note that in the thermal phase change model the evaporation-condensation mass transfer process is governed entirely by the interphase heat transfer processes and the overall heat balance. There is no calibration required for the mass transfer coefficients as there is in the Lee model. Therefore, it is generally recommended that you use the Eulerian multiphase formulation with the two-resistance heat transfer method when simulating evaporation-condensation processes.