The two-way coupling algorithm performs data exchanges between Rocky and Ansys Fluent at the begining of each Fluent time step. This means that both solvers continuously work with the previous results of the other; i.e., Rocky uses the Fluent solution from the previous time step to calculate both momentum and energy exchange with the fluid, while Fluent uses Rocky's solution from the previous time step to integrate the governing equations up to the next time step.
This coupling approach is numerically and computationally efficient as it reduces both the number of exchanges and possible stalls, which can happen when one of the solvers stops to wait for the other to complete its task. However, this approach may produce some instabilities when an inappropriate time step is chosen.
The Fluent solution uses a static particle map and source terms, which can be very limiting when modeling fast-paced processes, such as heat exchange at a high heat transfer rate or chemical reactions. The constant particle-related values Fluent uses during the time step solution in these cases can lead to very stiff problems, making the solution very difficult or even impossible to converge.
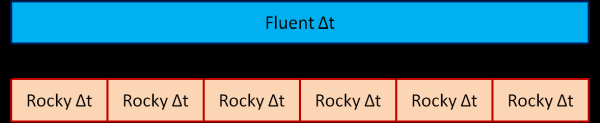
The Sub-stepping method implements a tighter interaction between Rocky and Fluent, by allowing multiple data exchanges between both solvers during a single Fluent time step. Figure 6.13: Sub-stepping algorithm. shows schematically the multiple data exchanges between the two solvers.
By making use of the Sub-stepping algorithm it is possible to increase the Fluent time step size resulting in a faster simulation with a very small impact on the coupling accuracy. This is possible because the multiple data exchanges within a single time step reduces the difference between the true time varying quantities, namely momentum and energy, and its static representation on both solvers during the asynchronous execution. On the other hand, keeping the Fluent time step size as originally set while making use of Sub-stepping can enhance the coupling stability. As a side effect, however, the simulation may take longer.
Due to the different integration schemes in both solvers, explicit for Rocky and implicit for Fluent, it is challenging to exchange data within a single Fluent time step, because Fluent is still performing non-linear iterations and it may not yet have achieved convergence. Therefore, Sub-stepping addresses the question of how and when to exchange data by determining:
Which fluid properties values are sent to Rocky when Fluent is still performing non-linear iterations.
How the Rocky source terms are imposed in Fluent within a Fluent time step.
What criterion is used to decided when to perform the data exchange.
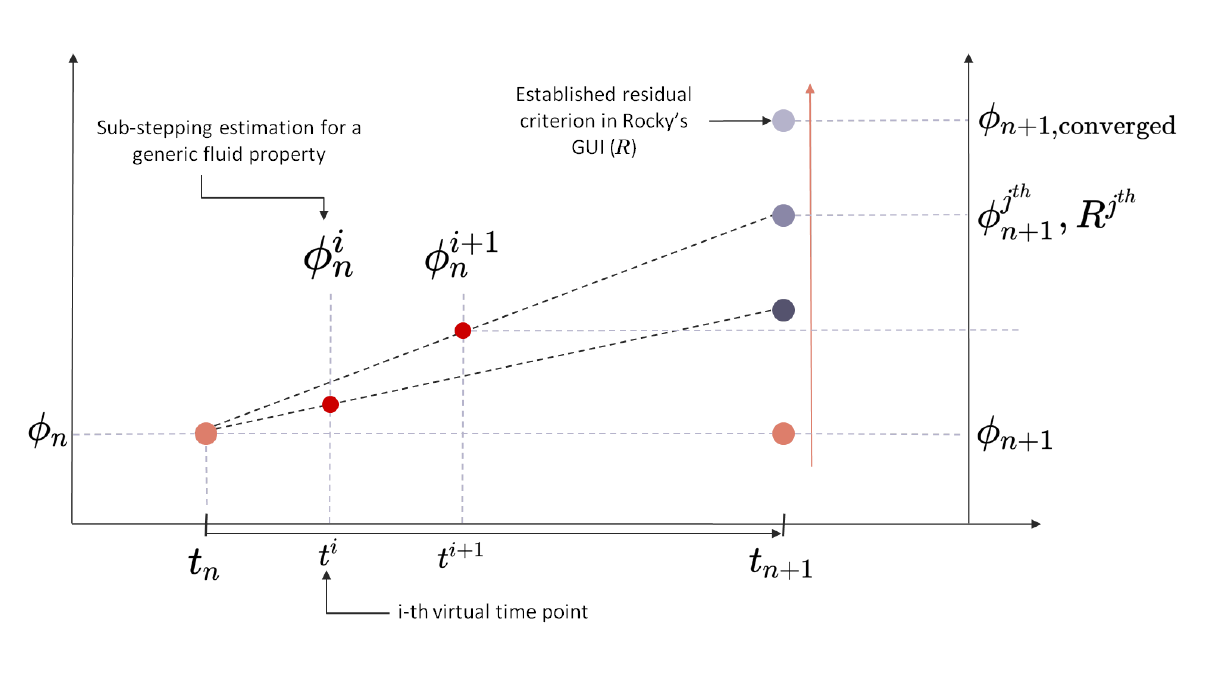
As an example, let us define a generic fluid property, , where i represents the i-th sub-step index, and
represents the current Fluent time step index. The Sub-stepping algorithm
performs a linear interpolation between the current non-converged property,
, and the converged property,
. Mathematically, this is given by:
(6–26) |
Where is the number of sub-steps defined by the user. Figure 6.14: Sub-stepping linear interpolation. shows the linear Sub-stepping interpolation.
Since is a non-converged fluid property, such as velocity, pressure, density,
etc., a new data exchange criterion based on the partial convergence of the CFD solution is
used for the Sub-stepping method. It is based on a modified convergence criterion of the
enabled Fluent equations, such as momentum, turbulence and energy to avoid additional
non-linear iterations that are not sensitive to the sub-stepping estimation. Therefore, the
standard convergence criteria on Fluent is relaxed by propagating the Fluent residuals
linearly into the i-th virtual time-point, which is a time-point within the
full time step size. The Sub-stepping exchange criteria is given by:
(6–27) |
Where is the maximum current computed residual value of all enabled equations in
Fluent,
is the i-th sub-step source term, and
is the Sub-stepping residual tolerance given by the user. It is important to
point out that for the last sub-step, namely
, the standard Fluent criterion is equivalent to the Sub-stepping criterion,
, meaning that all the equations have converged in case the maximum number of
iterations was not reached. The data exchange will also occur when the current Fluent
iteration number is equal to the maximum number of iterations set in Fluent divided by the
number of sub-steps.
Note that the fluid property depends on the source term provided by Rocky,
, which will vary along the non-linear iterations for the current time step.
The Sub-stepping method uses a weighted average to update the particle source terms in Fluent
given by:
(6–28) |
Where is the source sent by Rocky in the i-th sub-step, and
is the Sub-stepping weighted average used as the source term in Fluent.