The heat transfer rate between a particle and fluid, , can be calculated using Newton's law of cooling, which states that the rate
of heat loss of a body is directly proportional to the difference in the temperature between
the surface of the body and its surroundings.
Assuming that the heat transfer coefficient is relatively independent of the temperature difference between the body and the surroundings, the heat transfer hate is given by:
(4–2) |
where is the temperature of the particles surface,
is the local fluid temperature and
is the particle surface area.
The heat transfer coefficient depends upon fluid physical properties, as well as of the operating
conditions. For instance, for the same fluid and particles, turbulent flows give higher heat
transfer coefficients when compared to laminar flows. Therefore, a heat transfer coefficient
needs to be provided for the analyzed system.
In Rocky, the average convective heat transfer coefficient, , is calculated based on the Nusselt number,
, according to the expression:
(4–3) |
where is the fluid thermal conductivity and
is the equivalent diameter of the particle.
Different correlations can be found in the literature for calculating the Nusselt
number, usually in function of the Reynolds number, , and Prandtl number,
, defined as:
(4–4) |
where is the dynamic viscosity, and
is its specific heat.
The Ranz and Marshall (1952) [15], [14] correlation is valid for estimating the heat transfer between a spherical particle and its surroundings. The correlation is given:
(4–5) |
where is the relative Reynolds number based on the diameter of the particle
and the relative velocity and
is the Prandtl number, computed according to equation Equation 4–4 . The Ranz and Marshall correlation
is valid for
.
The correlation Whitaker (1972) [15], [13] is defined as:
(4–6) |
where is the viscosity of the fluid at the free stream temperature whereas
is the viscosity of the fluid at a temperature equal to the temperature
of the spheres surface.
The Whitaker correlation is suitable for the estimation of the Nusselt number for a
single spherical particle with Prandtl number within 0.7 < < 380, Reynolds number in the range of 3.5 <
< 76000, and viscosity ratio within 1 <
< 3.2.
For a no-flow condition, this correlation returns = 2, which is the estimation for steady radial pure conduction between a
spherical surface and the motionless, infinite, conducting medium that surrounds the
particle.
Gunn [12] derived a correlation for the Nusselt number based on analytical (simplified) solutions and four asymptotic relations that delineate the bounds of the Nusselt number for heat transfer to particles at low and high Reynolds number. These known asymptotic relations are:
The Nusselt number for a single particle at low Reynolds numbers.
The experimentally-established dependence of the Nusselt number for single particles.
The experimentally-established dependence of the Nusselt number for fixed beds at high Reynolds numbers.
A limiting value derived in the paper for low Reynolds numbers in a packed bed.
Using these relations, the derived expression is:
(4–7) |
where is the fluid volume fraction and
is the Reynolds number based on the fluid superficial velocity estimated
by Rocky as:
(4–8) |
The empirical correlation of Gunn (1978) is useful for calculating the heat
transfer rate in a fixed or fluidized bed of particles within the fluid volume fraction
range of , for gases and liquids, and for Reynolds numbers up to
.
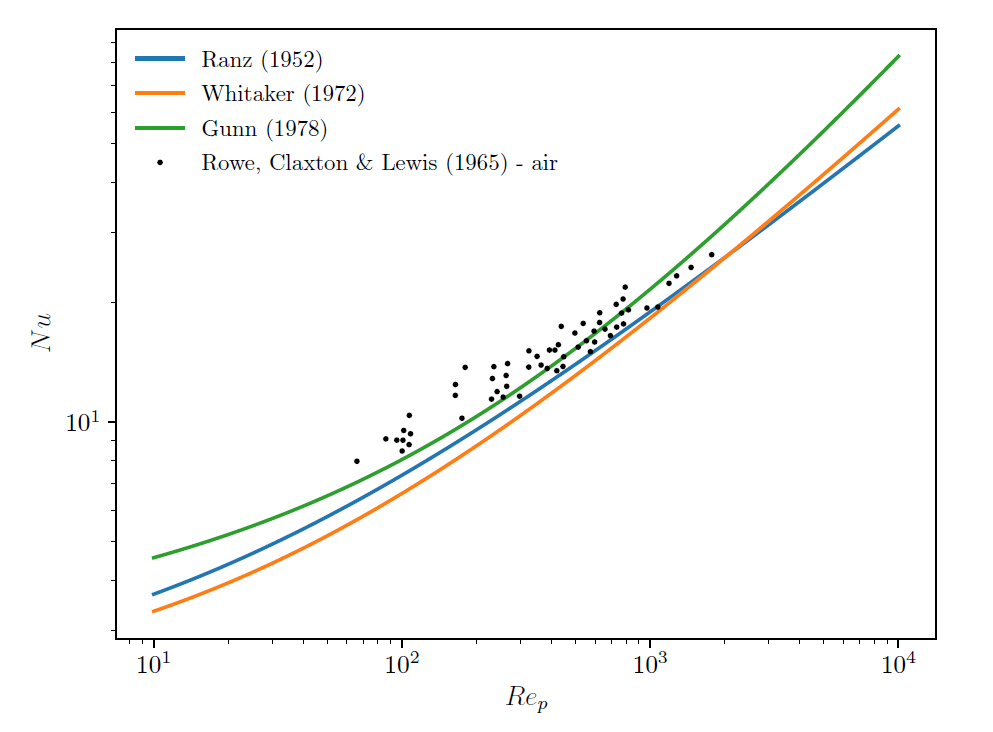
Figure Figure 4.1: Comparison of the Gunn correlation with and
to experimental data for fixed beds of spherical particles. shows a comparison of the Nusselt
number prediction using the correlation of Gunn (1978) and experimental results obtained by
different authors, for different Reynolds number values. [11],
[10], [9],[8].
Figure 4.1: Comparison of the Gunn correlation with and
to experimental data for fixed beds of spherical particles.
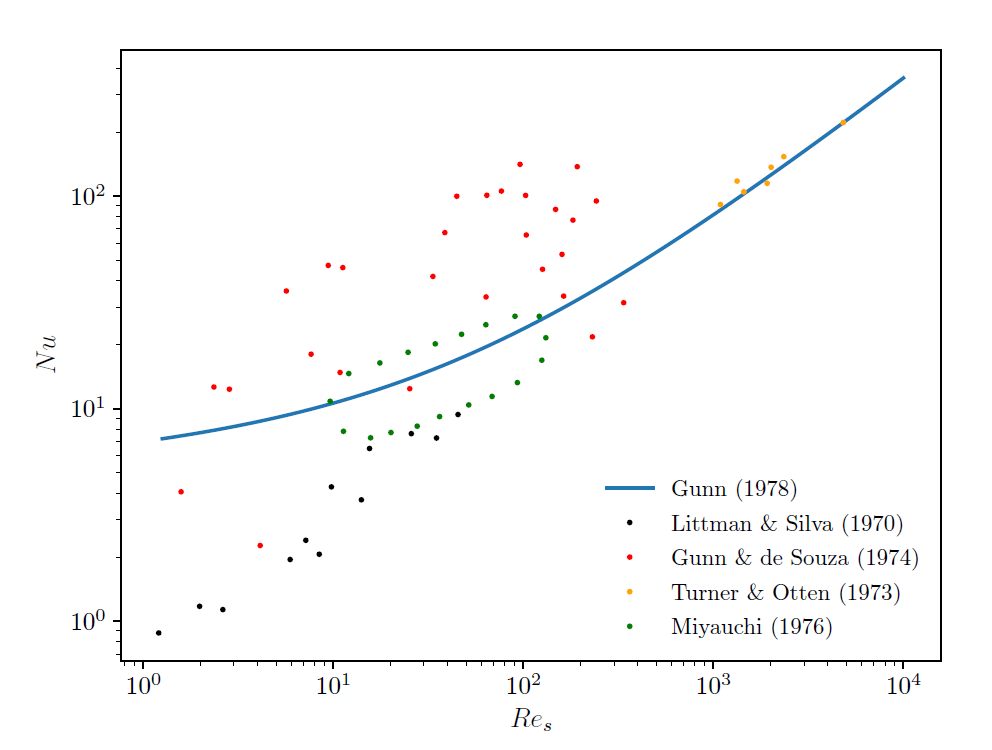
Figures Figure 4.2: Comparison of Nusselt number predictions of different correlations with to experimental data for a single spherical particle in water. and Figure 4.3: Comparison of Nusselt number predictions of different correlations with
to experimental data for a single spherical particle in air. compare the predictions of the Nusselt number using the
correlation of Ranz and Marshall (1952), Whitaker (1972) and Gunn (1978) to experimental
[7] data for a single spherical particle in water and air under
different Reynolds numbers.
Figure 4.2: Comparison of Nusselt number predictions of different correlations with to experimental data for a single spherical particle in water.
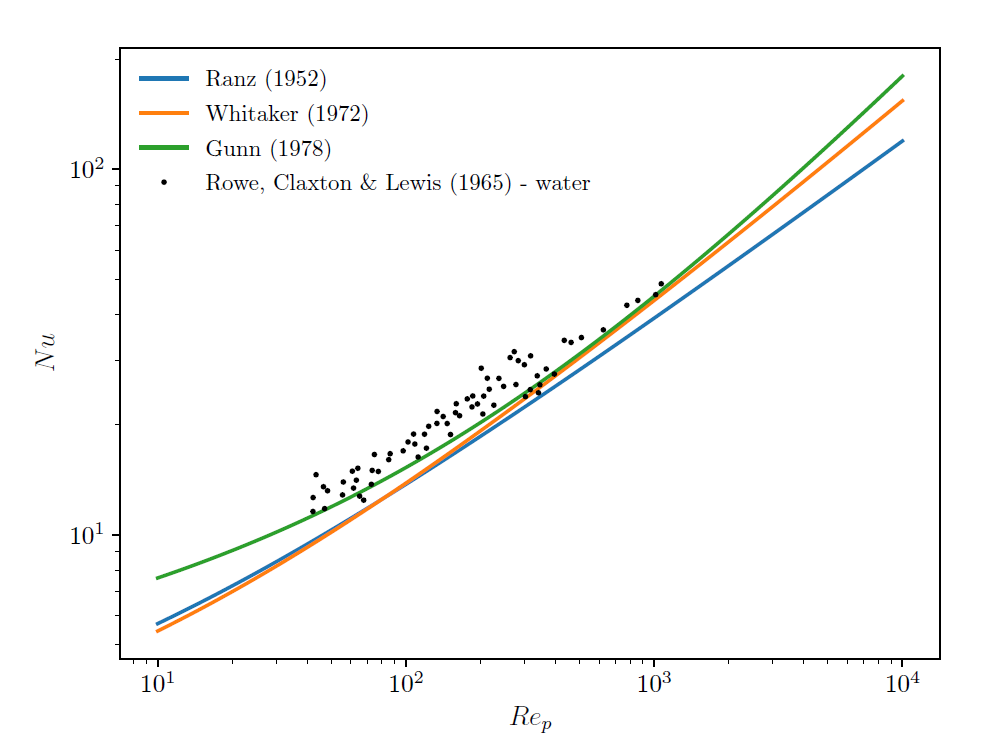
Figure 4.3: Comparison of Nusselt number predictions of different correlations with
to experimental data for a single spherical particle in air.