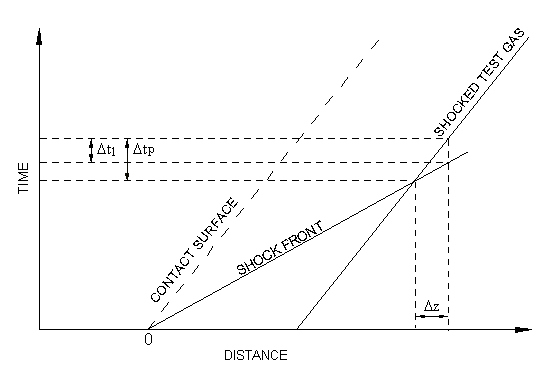
The experimentalist records changes in the test gas conditions (be it
pressure, temperature, density or species concentration) after passage of the shock at some
observation point. The time recorded on some external recording device is referred to as the
laboratory time, . Since the test gas is flowing
however, it has been at the post-shock conditions for some time longer than the laboratory
time. This longer time is referred to as the gas-particle time,
and is the time of interest with respect to rate processes in the test
gas. A relationship between
and
can be derived. To do so, begin by considering the distance-time diagram
in Figure 7.2: Laboratory and gas-particle times
. When the shock arrives at the
observation point, measurements are made on the test gas for a period
. The test gas has been at the shock-heated conditions for a time
and has traveled a distance
since being shocked. The time that it took the
shock wave to travel this same distance is
(
).
Hence, from the relationship between distance and time
(7–1) |
Taking the limit as approaches zero results in the following ordinary differential equation
relating gas particle and laboratory times:
(7–2) |
For mass continuity across the shock wave, it can be shown that
(7–3) |
and, therefore, Equation 7–2 can be written as
(7–4) |
Thus, when rate processes are measured, the time as measured must be multiplied by the density-area ratio across the shock to obtain the true rate referred to the test gas. In the Shock Reactor Model, Equation 7–4 is integrated along with the other ordinary differential equations (ODEs) presented in Downstream Model Equations , so that laboratory time as a function of gas-particle time is available. The Shock Reactor Model solves the coupled set of ODEs for either an incident or reflected shock problem.
The initial time for a problem, , is taken as the time immediately after the
shock wave has elevated the test gas to new levels of
temperature and pressure. The incident shock wave is assumed to instantaneously raise the
test gas from initial conditions 1 to conditions 2; the reflected shock is assumed to
instantaneously raise the test gas from conditions 2 to conditions 5. Gas composition
immediately after passage of the shock is assumed to remain unchanged from the initial
conditions. Vibrational and rotational energy relaxation processes are neglected.