As an example of a unimolecular/recombination fall-off reaction, consider
methyl recombination. In the high-pressure limit, the appropriate description of the
reaction is . In the low-pressure limit, a third-body collision is required to provide
the energy necessary for the reaction to proceed, that is, the appropriate description is
. When such a reaction is at either limit, the (solely
temperature-dependent) rate expressions discussed in the preceding paragraphs are
applicable. However, when the pressure and temperature are such that the reaction is between
the limits, the rate expressions are more complicated. To denote a reaction that is in this
"fall-off" region, we write the reaction with the positive + M enclosed in
parentheses,
(3–24) |
There are several methods of representing the rate expressions in this fall-off region. The simplest one is due to Lindemann [15]. There are also now two other (and related) methods that provide a more accurate description of the fall-off region than does the simple Lindemann form. The Gas-phase Kinetics package handles all three of these forms as options.
We begin with the Lindemann approach. Arrhenius rate parameters are
required for both the high- and low-pressure limiting cases, and the Lindemann form for the
rate coefficient relates them in a pressure-dependent rate expression. In Arrhenius form,
the parameters are given for the high-pressure limit and the low-pressure limit
as follows:
(3–25) |
(3–26) |
The rate constant at any pressure is then taken to be
(3–27) |
where the reduced pressure is given by
(3–28) |
and is the concentration of the mixture, possibly including enhanced
third-body efficiencies.
Note: It is also possible that the third body in the fall-off region could be a specific
species rather than the mixture as a whole. In such a case, the reaction could be written,
for example, as . In this case, the concentration of Nitrogen [N2
] would replace the total concentration in the mixture
in these equations.
For this example, note that the units for are 1/sec,
are cm6 /(mole2
⋅ sec2), and
are cm3 /(mole ⋅ sec). If the
in Equation 3–10
is unity, then this is the
Lindemann form. The other descriptions involve more complex expressions for the function
.
In the Troe form, [16] F is given by
(3–29) |
The constants in Equation 3–29 are
(3–30) |
(3–31) |
(3–32) |
and
(3–33) |
The four parameters ,
,
, and
must be specified as auxiliary input to the Gas-phase
Kinetics Pre-processor, as described in Neutral Third Body and Pressure
Dependent Parameters (Problems Having No Reactions
of
the Chemkin Input Manual
Input Manual). It
is often the case that the parameter
is not used. Thus Gas-phase Kinetics
provides for the use of either three or four parameters.
The approach taken at SRI International by
Stewart, et al. [18] is in many ways similar to that taken by Troe, but the blending function
is approximated differently. Here,
is given by
(3–34) |
where
(3–35) |
In addition to the six Arrhenius parameters—three each for the
low-pressure limit and high-pressure limit
expressions—the user must supply the parameters
,
, and
in the
expression. The parameters
and
were not discussed by Stewart, et al., but we have included them as
additional optional parameters to increase flexibility. If one wishes,
and
can be considered parameters that define a weak-collision efficiency
factor, in the event that one wants to compute strong-collision rate parameters and correct
them with such a factor.
Figure 3.1: Rate constant as a function of pressure at fixed temperature for a unimolecular fall-off reaction
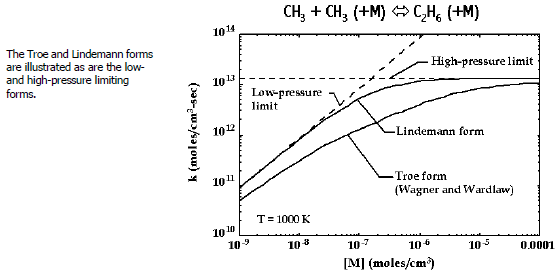
Figure 3.1: Rate constant as a function of pressure at fixed temperature for a unimolecular fall-off reaction
illustrates the pressure
dependence of rate expressions for the example reaction, , evaluated at a fixed temperature of 1000 K. Both the Lindemann and the
Troe forms are shown, as well as the low- and high-pressure limits. The specific constants
in fits to the Troe form (
,
,
,
,
,
,
,
,
) are taken from Wagner and Wardlaw [19]. For the relatively simple Lindemann case (
), the limiting behavior is apparent. In the low-pressure limit,
, the denominator in Equation 3–27
approaches unity and the rate
expression becomes
. In the high-pressure limit,
, the pressure-ratio factor approaches one, and the rate expression becomes
, that is, a constant. For both the Troe and SRI forms,
approaches unity for both high and low pressures. Thus, all expressions
recover the correct limiting behavior.


