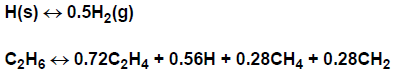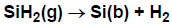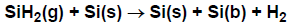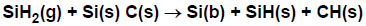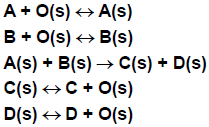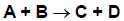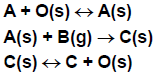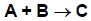The reversible (or irreversible) surface reactions that involve
chemical species and can be represented in the general form
(4–41) |
The stoichiometric coefficients for elementary reactions are integers and
is the chemical symbol for the kth species. Usually, an elementary reaction involves
only three or four species; hence the
matrix is quite sparse for a large set of reactions.
Global reactions are sometimes stated with non-integer stoichiometric coefficients. KINetics can accommodate non-integer stoichiometric coefficients.
The net production rate (in mole/cm2/sec) for each of the
species (regardless of phase) is the sum of the rate-of-production for all reactions involving the kth species
(4–42) |
where
(4–43) |
The rate-of-progress variable for the
th reaction is given by the difference of the forward rates and the reverse rates
(4–44) |
The production rate (in mole/cm2/sec) for each surface phase is
(4–45) |
where
(4–46) |
The term is the net change in number of surface sites of type
for surface reaction
. As discussed above, the form of the concentrations
depends upon whether species
is in the gas phase, on the surface, or in the bulk. Furthermore,
the units of the rate constants will depend on the reactants and products in a particular reaction.
As for gas-phase reactions, the forward rate constants for the
reactions are (by default) assumed to have the following Arrhenius temperature dependence
(4–47) |
where the pre-exponential factor , the temperature exponent
, and the activation energy
are specified. These three parameters are required input to the Surface Kinetics Pre-processor for each reaction. There are a number of ways in which the rate expression for a reaction
can be altered, which are summarized below.
Two gas constants, and
are used throughout this manual.
is used only in conjunction with the activation energy
and has compatible units. The reason for the duality is that many users would rather use different
units (for example, cal/mole) for the activation energies even though other units (for example, ergs/mole) are used elsewhere.
For reversible reactions, the reverse rate constants are related to the forward rate constants through the equilibrium constants as
(4–48) |
The user can over-ride the use of Equation 4–48 by
explicitly declaring Arrhenius coefficients for the reverse reaction in the Surface Kinetics
input via the auxiliary keyword REV.
Although is given in concentration units, the equilibrium constants are more easily
determined from the thermodynamic properties in pressure units,
. They are related by
(4–49) |
where denotes a pressure of 1 atm, and
is the standard-state surface site density of site type
. The sum in the first exponent runs only over the gas-phase species, and the sum in
the second exponent runs only over surface species in surface phase
. The equilibrium constant
is obtained from the standard-state Gibbs free energy of reaction,
(4–50) |
For many real-world applications the elementary reactions are not known. Instead, the kinetics may only be summarized in terms of global expressions. Gas-phase Kinetics and Surface Kinetics input may therefore include use of non-integer stoichiometric coefficients.
The rate-of-progress of a reaction is, by default, still evaluated via
Equation 4–44, with the coefficients
and
defined as real numbers instead of integers. The Gas-phase Kinetics and
Surface Kinetics Pre-processors automatically allow real coefficients for reactions
without requiring any special flags or keywords.
By default the rate-of-progress of a reaction is evaluated by Equation 4–44, which uses the concentration of each reactant or product species raised to the power of its stoichiometric coefficient. Thus, the rate-of-progress of a reaction that includes species A with a coefficient of 2 will be second-order with respect to the concentration of A. Equation 4–44 would always be valid when mass-action kinetics are obeyed, and the mechanism is written in terms of elementary reactions.
However, often in real-world applications the elementary kinetics are not known. In some
cases, an experimental measurement finds that the rate of reaction is proportional to the
concentration of a species raised to some arbitrary power (different from its
stoichiometric coefficient). Using the arbitrary-reaction-order option, the user may
declare that the rate-of-progress of a reaction is proportional to the concentration of
any species (regardless of whether that species even appears as a reactant or a product in
the reaction) raised to any specified power. To modify the reaction order for the reaction
in the forward or reverse direction, the user must declare the FORD
or RORD auxiliary keywords, respectively, in the input file, as
described in the Chemkin Input Manual.
When the reaction-order-dependence of reaction is changed via the
FORD or RORD auxiliary keywords,
the rate-of-progress variable for the reaction is evaluated by:
(4–51) |
where is the reaction order specified through the
FORD keyword and is the reaction order specified through the
RORD keyword for species . The default for species participating in reaction
is the normal mass-action kinetics values:
(4–52) |
(4–53) |
if an order-change parameter is not given for species participating in that reaction.
The user is advised to exercise caution when specifying a change of reaction order. Such a change may produce unexpected and unphysical results in a kinetic simulation. The user should also consider the kinetics of the reverse reaction when changing reaction-orders for the forward reaction. For example, such a reaction may no longer satisfy microscopic reversibility. At equilibrium, elementary kinetics ensure that
(4–54) |
A reaction for which one has specified an arbitrary reaction order will not have the proper equilibrium behavior unless
(4–55) |
The user specifying may also wish to adjust
such that Equation 4–55 is
satisfied; the software does not do this automatically. Another alternative would be to
simply specify that the reaction is irreversible, in which case the details of the reverse
reaction become irrelevant.
In some cases there are experimental data that indicate that the Arrhenius expression for the
rate constant, Equation 4–47, is modified by the
coverage (concentration) of some surface or bulk species. The user may specify optional
coverage parameters for species and reaction
, through use of the auxiliary keyword
COV. In this
case, the rate constant for the forward reaction is modified as
(4–56) |
where the three coverage parameters are ,
, and
for species
and reaction
. The product in Equation 4–56
runs over only those surface species that are specified as contributing to the coverage
modification. Note that the surface site fractions appear in Equation 4–56 rather than molar concentrations
(mole/cm2) for surface species, while bulk activities appear for bulk species. The term associated
with
now makes it possible for the rate-of-progress of a reaction to be proportional
to any arbitrary power of a surface species concentration. Also, using this modified
expression for
, the net pre-exponential factor may be a function of coverage
(4–57) |
and the activation energy is a function of the coverage
(4–58) |
For reactions with optional coverage dependence, the rate of progress is calculated employing Equation 4–44, with the forward rate coefficient from Equation 4–56.
If the form of Equation 4–56 is not flexible enough to describe a certain coverage behavior, one can repeat the same reaction several times with different values for the coverage parameters such that the sum of the rate constants approximates the desired form.
For some simple surface reaction mechanisms we have found it convenient to specify the surface reaction rate constant in terms of a “sticking coefficient” (probability).
Because is defined as a probability, it must lie between 0 and 1 to make physical sense.
Therefore, KINetics checks the value of
, and an unphysical sticking
coefficient greater than 1 is changed to the value 1.
For example, one might have a measurement or intuition about the probability that a certain process takes place when a given collision occurs. For consistency in expressing each surface reaction in terms of a rate constant, we provide a conversion between this sticking coefficient form and the usual rate expression. We allow the sticking coefficient form only for the simple case of a surface reaction in which there is exactly one gas-phase reactant species, although there can be any number of surface species specified as reactants.
The sticking coefficient's functional form is taken to be
(4–59) |
In this case, and
are unitless and
has units compatible with
. KINetics also allows for surface-coverage modification of a sticking
coefficient, analogous to Equation 4–56.
We give three successively complex examples of using sticking coefficients. First, to specify
that SiH2(g) reacts with probability upon each collision with the surface, one could write the reaction as in
Figure 4.7: Example of sticking-coefficient reaction with no surface species.
In this example, we have not explicitly included the surface in writing the reaction.
A somewhat more detailed way of using the sticking-coefficient specification would be to say
that SiH2(g) reacts with probability upon each collision with a bare surface silicon atom, Si(s), as in
Figure 4.8: Example of sticking-coefficient reaction with a surface site.
If the surface site fraction of Si(s) were unity, then a fraction of the collisions of SiH2
with the surface would result in a reaction. However, for Si(s) coverages less than 1,
the reaction rate decreases in proportion with the coverage of Si(s).
In a third (contrived) example, suppose there is a probability for a reaction to occur when SiH2 collides with
both a Si(s) and a C(s) site, as in Figure 4.9: Example of sticking-coefficient reaction with multiple surface sites.
The rate of this reaction would be proportional to both the coverage of Si(s) and C(s).
To convert rate constants given as sticking coefficients to the usual mass-action kinetic rate constants there is the relation
(4–60) |
where is the universal gas constant,
is the molecular weight of the gas-phase species,
is the total surface site concentration summed over all surface phases
(number of moles of surface sites per unit area), and
is the sum of all the stoichiometric coefficients of reactants that are
surface species. The term involving
raised to the
power is needed to convert from the unitless sticking coefficient form
to units appropriate for a rate constant, and the term in the square root accounts for the
gas/surface collision frequency. In the third example given above,
Equation 4–9, the value of
is 2, because there are two surface sites appearing as reactants, in
other words, Si(s) and C(s). The product term in Equation 4–60 is the product of the site-species occupancies, raised to a
power equal to the reaction order for that species, for all site species that are
reactants. Here,
is the number of sites that the surface species occupies, and
is the reaction order for that species. The product term will be equal
to one when there are unity site occupancies for all of the surface species in the
reaction.
Implicit in the sticking coefficient description just presented is an assumption that the sticking coefficient is relatively small, that is, much less than one. In this case the molecular motion in the vicinity of the solid surface is random and the collision frequency of gas-phase species with the surface is not affected by the surface itself. However, when the sticking coefficient is large, in other words, close to one, then the velocity distribution becomes skewed. Species whose random motion carries them close to the surface have a high probability of staying there, which causes a non-Maxwellian velocity distribution that, in turn, alters the net species flux near the surface.
Motz and Wise [18] analyzed this situation and provided a correction factor that modified Equation 4–60 as
(4–61) |
The rate-of-progress is calculated using Equation 4–44, as usual. The sticking coefficient specification is only allowed for the forward reaction. If the reaction is written as reversible, the reverse reaction rate constant would be calculated from Equation 4–61 and Equation 4–48 using microscopic reversibility.
Surface reactions are often described using global reactions rather than as a series of elementary reactions. Some of the most common global rate expressions used for surface reactions are the Langmuir-Hinshelwood (LH) and Eley-Rideal (ER) rate expressions. LH applies to the case where adsorption and desorption are assumed to be in equilibrium, and a reaction on the surface between adsorbed species is rate determining. ER applies to the case of a reaction between a gas-phase species and an adsorbed species being rate-limiting. Although originally developed for specific cases, these names are now used to refer to a variety of rate expressions with similar forms. If an LH reaction is used, a single global reaction might constitute the entire surface chemistry mechanism. The "Langmuir" part of the name for the LH rate expression originates from the inclusion of the Langmuir adsorption isotherm, which assumes that the adsorption sites on the surface are independent from each other (single site adsorption), the sites are equivalent, and the surface coverage decreases the number of sites available for adsorption only, but does not alter the energetics of adsorption/desorption.
The following example of an LH reaction illustrates its features. Species A and B co-adsorb onto the surface, react to products C and D, which can then desorb. The reaction between adsorbed A and adsorbed B is assumed to be rate-limiting and irreversible, while the adsorption/desorption processes are assumed to be in equilibrium. In the LH formulation, the elementary chemical reactions shown in Figure 4.10: Langmuir-Hinshelwood elementary chemical reactions would be replaced by the single overall reaction shown in Figure 4.11: Langmuir-Hinshelwood single overall reaction, which does not explicitly include any surface species.
The effects of surface sites being blocked by various species are included via the adsorption/desorption equilibria. This "lumping" of a number of elementary steps together results in a rate expression that differs substantially from a simple mass-action rate expression. The rate of progress variable is given by:
(4–62) |
where the is the equilibrium constant in each adsorption/desorption steps and
is the concentration of the species. As product species, C and D do not
appear in the numerator, but as adsorbed species they can block surface sites, so they do
appear in the denominator. The
is expressed in terms of Arrhenius parameters, as is
. The equilibrium constant is defined as
, in parallel with the standard expression for rate constants. Often, the
equilibrium constants in the numerator are lumped into the rate constant, giving:
(4–63) |
The generalized form of the above expression is:
(4–64) |
where represents gas-phase species in the reaction, and the exponent of 2 in
the denominator comes from the fact that the reaction rate is determined by the reaction
between two adsorbed species. In practice, this rate form is often used for empirical
parameter fitting, so we further generalize it to:
(4–65) |
where:
The chemical species in the rate law are not limited to the reactants and products in the reaction description
The exponents (
) for the chemical species concentrations in the numerator of Equation 4–65 may differ from the stoichiometric coefficients (
) and may be fractional
The overall exponent in the denominator (
) of may differ from 2, and may be fractional
The exponents (
) for the concentrations of species in the denominator may differ from 1 or the stoichiometric coefficients, and may be fractional
Eley-Rideal (also called Rideal-Eley) reactions are less common than LH reactions. The following example illustrates their features. Species A adsorbs onto the surface, then reacts with gas-phase species B to produce C, which can then desorb. The reaction between adsorbed A and gas-phase B is assumed to be rate-limiting and irreversible, while the adsorption/desorption processes are assumed to be in equilibrium. In the ER formulation, the elementary chemical reactions shown in Figure 4.12: Eley-Rideal elementary chemical reactions would be replaced by the single overall reaction shown in Figure 4.13: Eley-Rideal single overall reaction, which does not explicitly include any surface species.
In this case, the rate of progress variable is given by:
(4–66) |
or
(4–67) |
The generalized form of this is:
(4–68) |
which is the same as the Equation 4–64,
above, for LH kinetics, except that the denominator has an overall exponent
() of one rather than two. ER reactions are thus treated as a special case
of the LH rate law.
Using the LH option requires paying careful attention to the units of the reaction
rates. The discussion above assumes that the rate expressions are given in terms of gas
concentrations, which is the standard for Gas-phase Kinetics. However, literature values
for LH rate parameters, especially equilibrium constants, are often provided in pressure
units. To reduce the number of units conversions required, equilibrium constants may be
input in either pressure units or concentration units. This option is currently limited to
the LH rate expression and only for the equilibrium
constants. Rate parameters still must be input in concentration units. In Surface Kinetics
input, the default units, unless altered on the REACTION line, for
the rate of a reaction are moles
cm-2sec-1. Rate parameters given in
pressure units, for example in atm sec-1, do not have the same
dimensions as moles cm-2sec-1. Such
a rate would need to be divided both by and the surface-area to volume ratio (
), before use. Rates given in terms of weight of catalyst need to be
converted to a rate expressed in terms of the effective surface area of the catalyst via
the surface area per unit weight of catalyst and the dispersion. Rates given on a per-site
basis should also be converted to a per-area basis.